Sort Points on 2d Plane to Draw Lines Between Them

Applied Deep Learning - Part 1: Bogus Neural Networks

Overview

Welcome to the Practical Deep Learning tutorial series. We will do a detailed analysis of several deep learning techniques starting with Bogus Neural Networks (ANN), in particular Feedforward Neural Networks. What separates this tutorial from the remainder you tin notice online is that we'll accept a hands-on approach with plenty of code examples and visualization. I won't go into too much math and theory behind these models to continue the focus on application.

We will use the Keras deep learning framework, which is a high level API on top of Tensorflow. Keras is becoming super popular recently because of its simplicity. It'southward very easy to build complex models and iterate rapidly. I also used barebone Tensorflow, and actually struggled quite a bit. Subsequently trying out Keras I'1000 non going back.

Here'south the table of contents. First an overview of ANN and the intuition behind these deep models. And then we volition commencement simple with Logistic Regression, mainly to get familiar with Keras. Then we will train deep neural nets and demonstrate how they outperform linear models. Nosotros will compare the models on both binary and multiclass classification datasets.

ANN Overview
1.1) Introduction
1.ii) Intuition
i.3) Reasoning
Logistic Regression
2.1) Linearly Separable Data
2.2) Complex Data - Moons
2.3) Circuitous Data - Circles
Bogus Neural Networks (ANN)
3.i) Circuitous Data - Moons
3.2) Complex Information - Circles
iii.iii) Complex Data - Sine Moving ridge
Multiclass Nomenclature
4.1) Softmax Regression
4.2) Deep ANN
Conclusion

The code for this commodity is bachelor hither equally a Jupyter notebook, feel costless to download and try it out yourself.

I remember y'all'll learn a lot from this article. You lot don't need to take prior knowledge of deep learning, only some bones familiarity with full general machine learning. So let's begin…

1. ANN Overview

1.1) Introduction

Artificial Neural Networks (ANN) are multi-layer fully-connected neural nets that await similar the figure below. They consist of an input layer, multiple subconscious layers, and an output layer. Every node in ane layer is connected to every other node in the side by side layer. We make the network deeper past increasing the number of hidden layers.

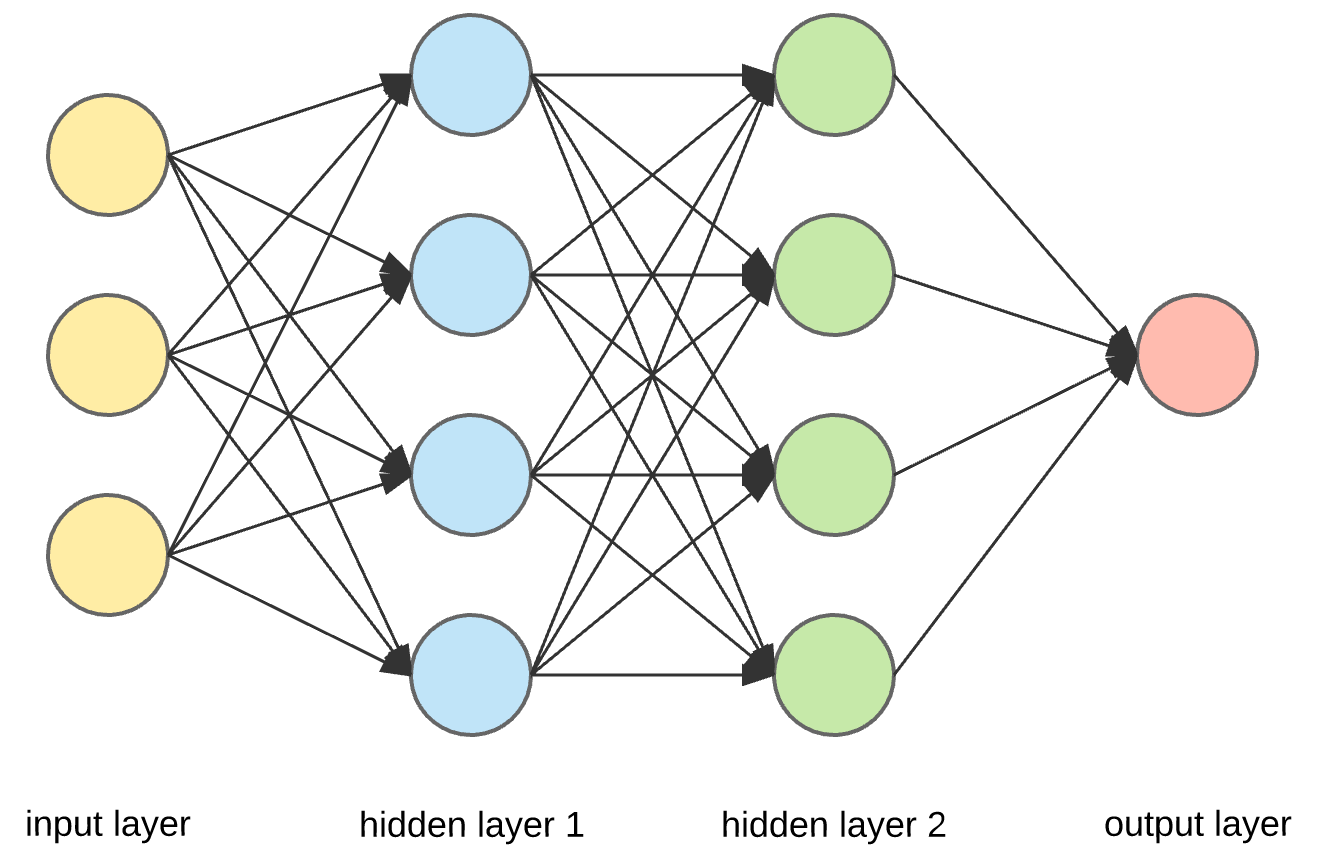
If we zoom in to one of the hidden or output nodes, what we will encounter is the effigy below.

A given node takes the weighted sum of its inputs, and passes it through a non-linear activation function. This is the output of the node, which and then becomes the input of another node in the next layer. The indicate flows from left to right, and the final output is calculated by performing this process for all the nodes. Training this deep neural network ways learning the weights associated with all the edges.

The equation for a given node looks as follows. The weighted sum of its inputs passed through a non-linear activation function. It tin can exist represented as a vector dot product, where n is the number of inputs for the node.

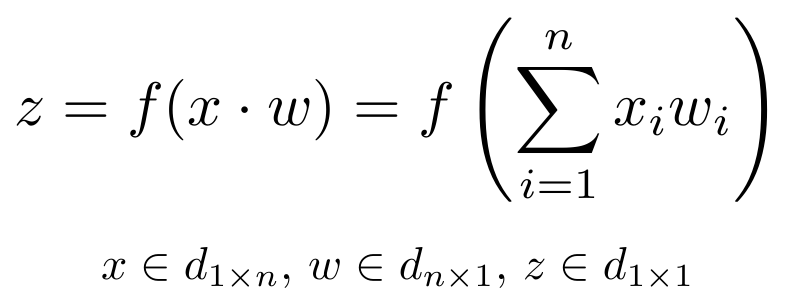
I omitted the bias term for simplicity. Bias is an input to all the nodes and always has the value 1. It allows to shift the result of the activation function to the left or right. It also helps the model to train when all the input features are 0. If this sounds complicated right now you tin can safely ignore the bias terms. For completeness, the above equation looks as follows with the bias included.

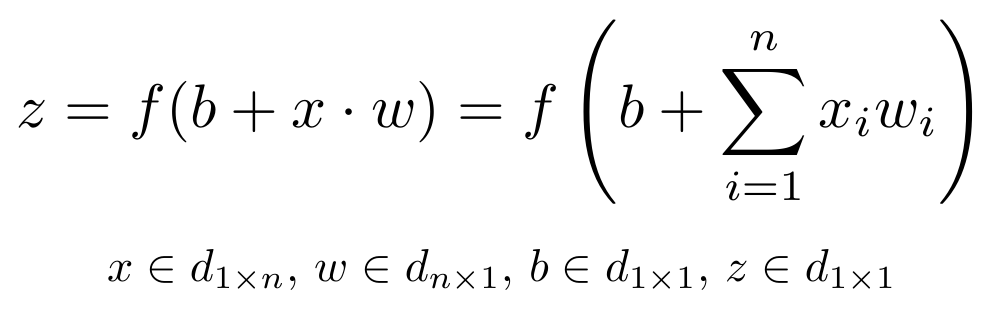
So far we have described the forward pass, meaning given an input and weights how the output is computed. After the training is complete, we only run the frontward laissez passer to make the predictions. But we beginning need to train our model to actually learn the weights, and the preparation procedure works equally follows:

Randomly initialize the weights for all the nodes. There are smart initialization methods which we will explore in another article.
For every preparation example, perform a forward pass using the electric current weights, and calculate the output of each node going from left to right. The last output is the value of the last node.
Compare the last output with the actual target in the training information, and measure the error using a loss function.
Perform a backwards pass from right to left and propagate the error to every private node using backpropagation. Summate each weight's contribution to the mistake, and accommodate the weights accordingly using gradient descent. Propagate the error gradients back starting from the last layer.

Backpropagation with gradient descent is literally the "magic" behind the deep learning models. It'southward a rather long topic and involves some calculus, and then we won't get into the specifics in this practical deep learning serial. For a detailed caption of gradient descent refer here. A bones overview of backpropagation is available hither. For a detailed mathematical handling refer hither and hither. And for more advanced optimization algorithms refer here.

In the standard ML world this feed forrard architecture is known as the multilayer perceptron. The difference between the ANN and perceptron is that ANN uses a non-linear activation function such as sigmoid but the perceptron uses the step role. And that non-linearity gives the ANN its great power.

ane.2) Intuition

In that location's a lot going on already, even with the basic forwards pass. Now let's simplify this, and sympathize the intuition behind it.

Essentially what each layer of the ANN does is a non-linear transformation of the input from one vector space to another.

Permit's use the ANN in Effigy i to a higher place as an case. We have a 3-dimensional input corresponding to a vector in 3D space. We then pass it through ii subconscious layers with 4 nodes each. And the final output is a 1D vector or a scalar.

And so if we visualize this as a sequence of vector transformations, we first map the 3D input to a 4D vector infinite, then nosotros perform another transformation to a new 4D infinite, and the final transformation reduces it to 1D. This is just a chain of matrix multiplications. The frontward laissez passer performs these matrix dot products and applies the activation office chemical element-wise to the result. The figure below just shows the weight matrices being used (not the activations).

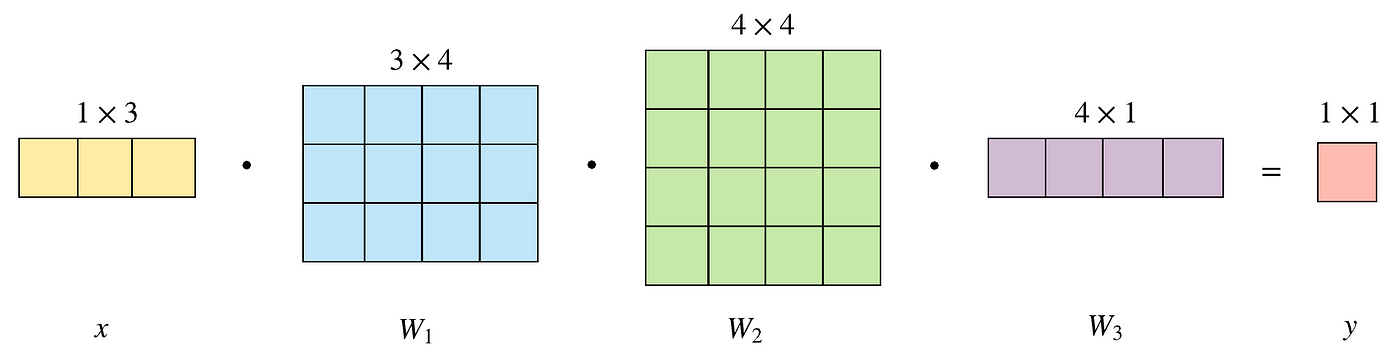
The input vector x has one row and 3 columns. To transform information technology into a 4D space, nosotros need to multiply it with a 3x4 matrix. And so to some other 4D space, we multiply with a 4x4 matrix. And finally to reduce it to a 1D space, we utilize a 4x1 matrix.

Notice how the dimensions of the matrices stand for the input and output dimensions of a layer. The connection between a layer with 3 nodes and four nodes is a matrix multiplication using a 3x4 matrix.

These matrices represent the weights that define the ANN. To brand a prediction using the ANN on a given input, we but demand to know these weights and the activation function (and the biases), nada more. We railroad train the ANN via backpropagation to "learn" these weights.

If we put everything together information technology looks like the figure below.

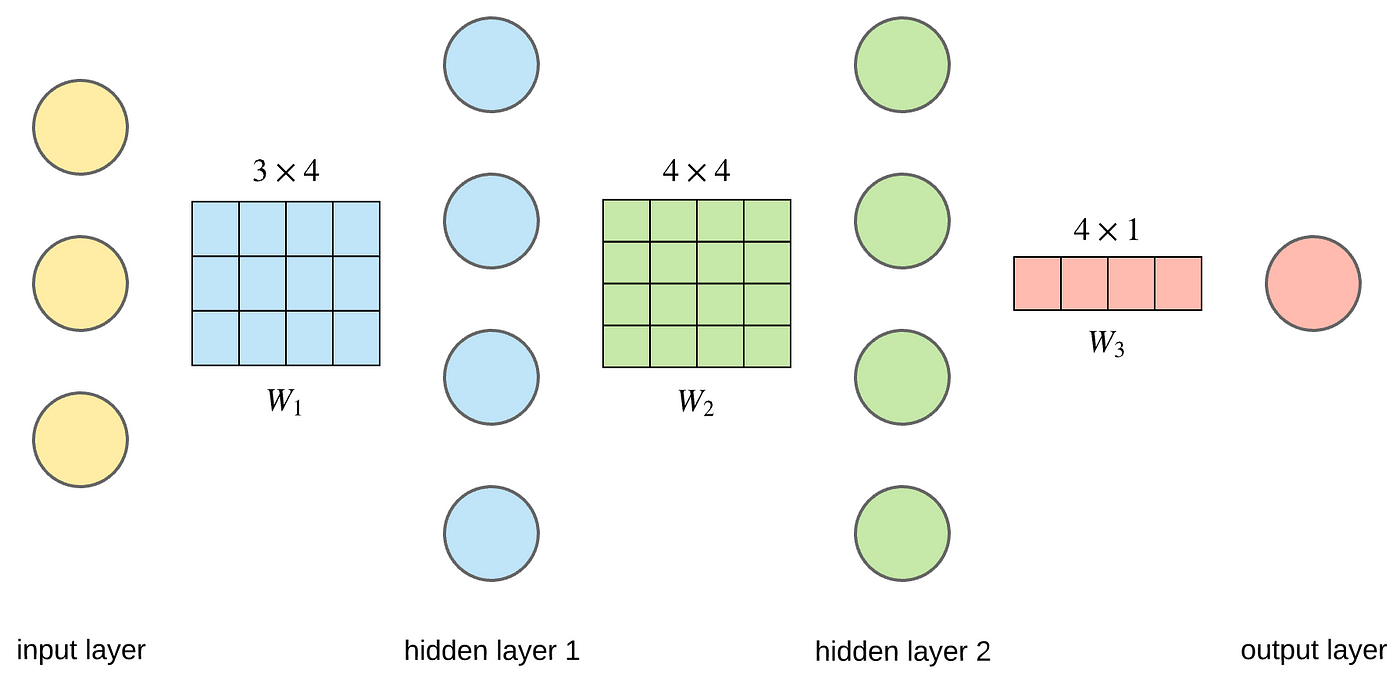
A fully continued layer between 3 nodes and 4 nodes is just a matrix multiplication of the 1x3 input vector (yellowish nodes) with the 3x4 weight matrix W1. The consequence of this dot product is a 1x4 vector represented as the blueish nodes. We so multiply this 1x4 vector with a 4x4 matrix W2, resulting in a 1x4 vector, the green nodes. And finally a using a 4x1 matrix W3 nosotros go the output.

We have omitted the activation function in the above figures for simplicity. In reality later every matrix multiplication, we utilise the activation function to each element of the resulting matrix. More formally

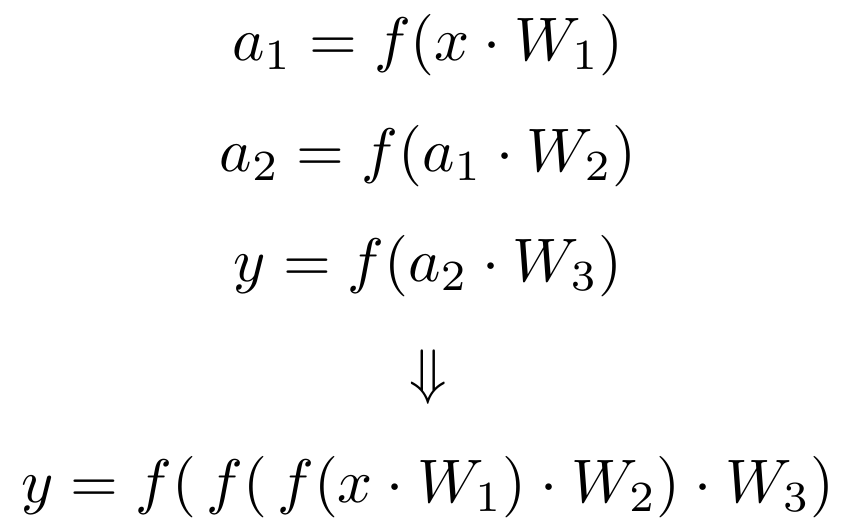
The output of the matrix multiplications go through the activation role f. In case of the sigmoid function, this means taking the sigmoid of each element in the matrix. We can see the chain of matrix multiplications more than clearly in the equations.

1.3) Reasoning

Then far we talked about what deep models are and how they work, but why practice nosotros need to go deep in the get-go identify?

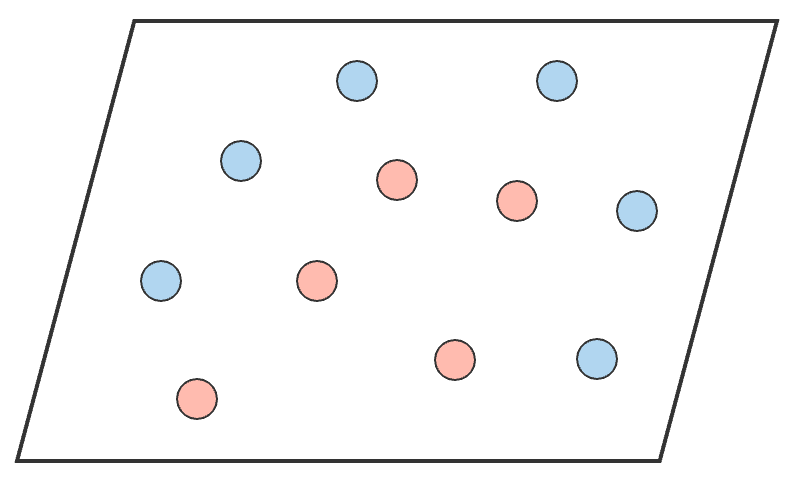
We saw that a layer of ANN merely performs a non-linear transformation of its inputs from one vector space to another. If we take a nomenclature problem as an example, we want to separate out the classes by drawing a decision purlieus. The input data in its given form is not separable. Past performing non-linear transformations at each layer, we are able to project the input to a new vector space, and draw a complex decision boundary to separate the classes.

Let'southward visualize what we just described with a concrete instance. Given the following data we can see that it isn't linearly separable.

So nosotros projection it to a higher dimensional space by performing a non-linear transformation, and then information technology becomes linearly separable. The green hyperplane is the conclusion purlieus.

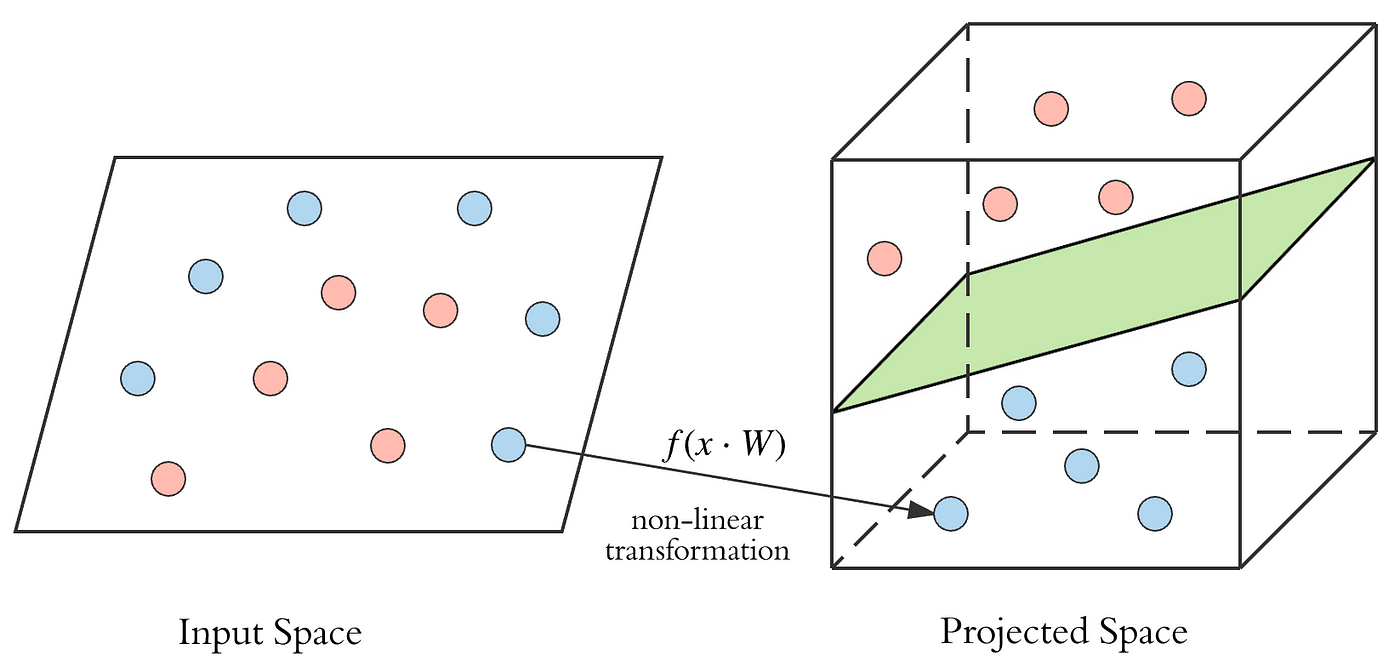
This is equivalent to cartoon a complex decision boundary in the original input infinite.

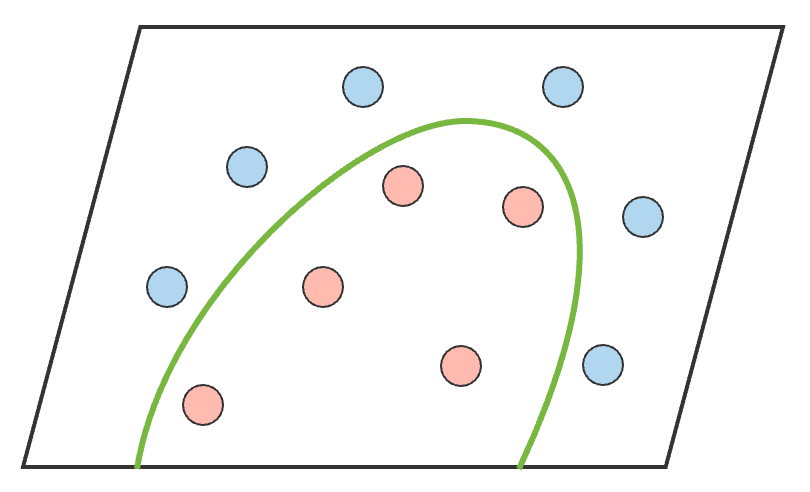
So the main benefit of having a deeper model is being able to do more non-linear transformations of the input and drawing a more complex decision boundary.

Every bit a summary, ANNs are very flexible yet powerful deep learning models. They are universal function approximators, meaning they can model any complex function. At that place has been an incredible surge on their popularity recently due to a couple of reasons: clever tricks which made training these models possible, huge increase in computational power especially GPUs and distributed training, and vast amount of grooming data. All these combined enabled deep learning to gain significant traction.

This was a brief introduction, at that place are tons of great tutorials online which cover deep neural nets. For reference, I highly recommend this newspaper. Information technology'due south a fantastic overview of deep learning and Section 4 covers ANN. Another cracking reference is this book which is available online.

2. Logistic Regression

Despite its name, logistic regression (LR) is a binary classification algorithm. It's the most popular technique for 0/1 classification. On a 2 dimensional (2nd) information LR will endeavour to draw a direct line to separate the classes, that'due south where the term linear model comes from. LR works with whatsoever number of dimensions though, non merely two. For 3D information it'll endeavour to draw a second aeroplane to separate the classes. This generalizes to N dimensional data and Northward-1 dimensional hyperplane separator. If you lot accept a supervised binary nomenclature trouble, given an input data with multiple columns and a binary 0/i result, LR is the first method to try. In this section we will focus on 2D data since it'south easier to visualize, and in another tutorial nosotros volition focus on multidimensional input.

one.one) Linearly Separable Data

First let'southward start with an easy example. 2d linearly separable data. We are using the scikit-learn make_classification method to generate our data and using a helper function to visualize it.

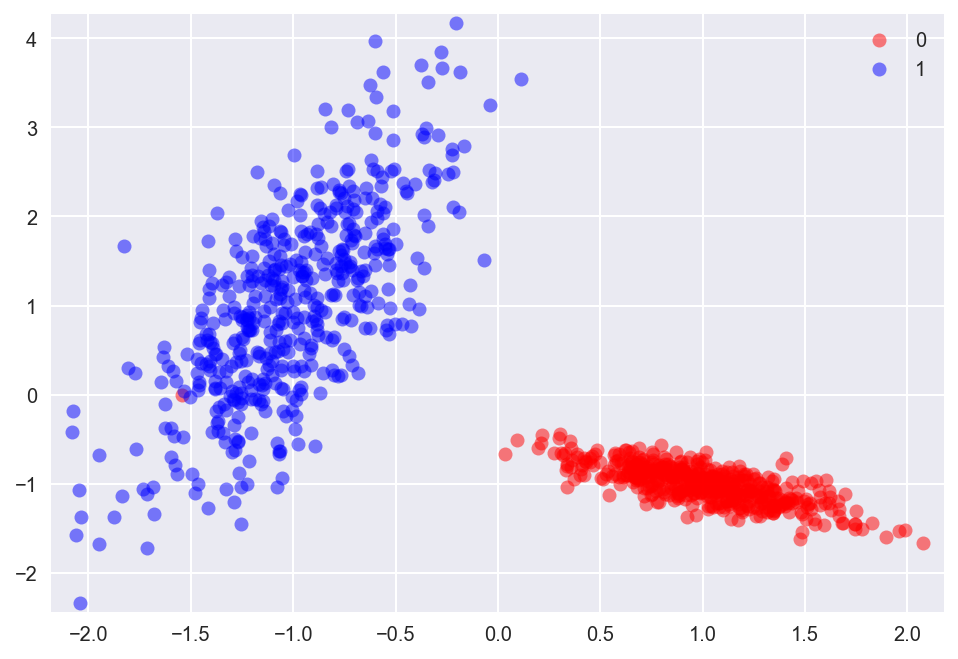
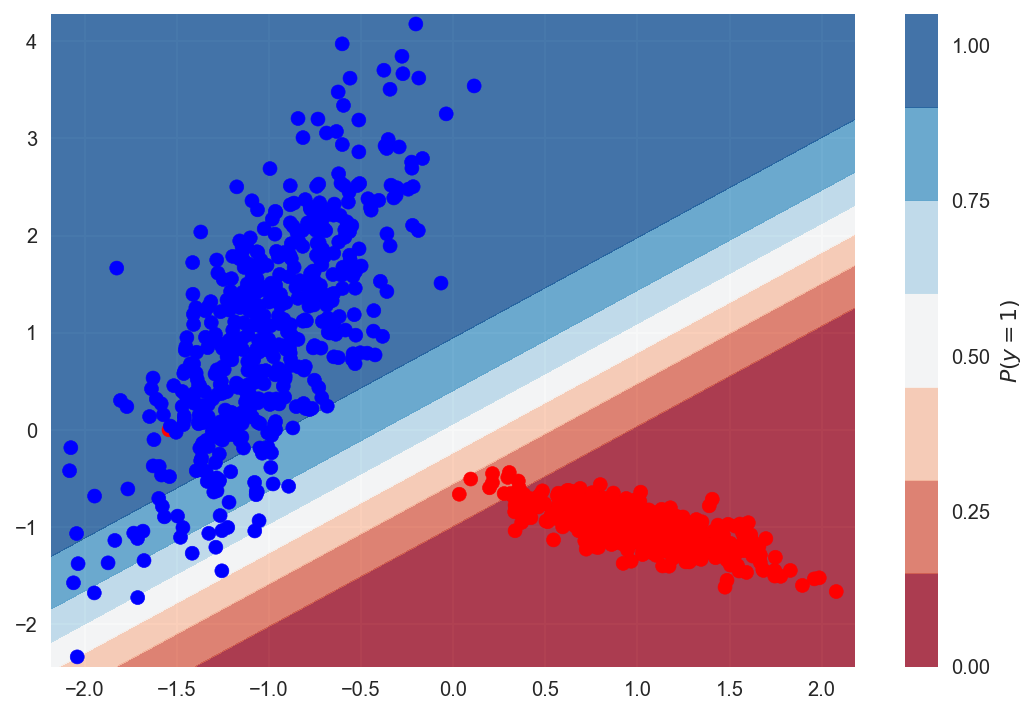
There is a LogisticRegression classifier bachelor in scikit-learn, I won't become into as well much detail here since our goal is to learn building models with Keras. But here's how to train an LR model, using the fit function just like any other model in scikit-larn. Nosotros see the linear conclusion boundary as the greenish line.

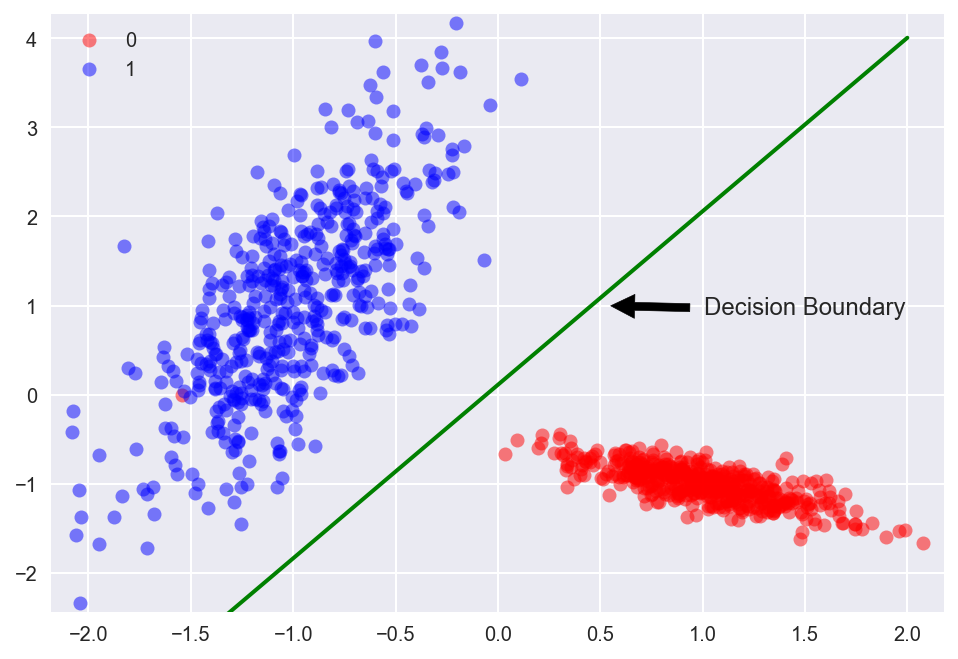
As we can see the data is linearly separable. We will at present train the aforementioned logistic regression model with Keras to predict the grade membership of every input indicate. To keep things simple for now, we won't perform the standard practices of separating out the data to grooming and examination sets, or performing grand-fold cross-validation.

Keras has great documentation, cheque it out for a more detailed description of its API. Hither'due south the lawmaking for preparation the model, allow'south go over it footstep by stride below.

We volition utilise the Sequential model API available here. The Sequential model allows us to build deep neural networks by stacking layers i on top of another. Since we're now building a simple logistic regression model, we will have the input nodes direct connected to output node, without any hidden layers. Annotation that the LR model has the course y=f(xW) where f is the sigmoid office. Having a single output layer existence directly connected to the input reflects this function.

Quick clarification to disambiguate the terms being used. In neural networks literature, it'due south common to talk about input nodes and output nodes. This may sound strange at first glance, what's an input "node" per se? When nosotros say input nodes, we're talking about the features of a given preparation example. In our case we have 2 features, the x and y coordinates of the points we plotted above, so we have two input nodes. You can just call back of it every bit a vector of 2 numbers. What about the output node then? The output of the logistic regression model is a unmarried number, the probability of an input information point belonging to class 1. In other words P(class=1). The probability of an input betoken belonging to class 0 is and then P(class=0)=one−P(course=ane). And then yous can simply think of the output node as a vector with a single number (or only a scalar) between 0 and 1.

In Keras nosotros don't add layers corresponding to input nodes, nosotros but exercise for subconscious and output nodes. In our current model, we don't have whatever hidden layers, the input nodes are directly connected to the output node. This means our neural network definition in Keras volition merely have one layer with i node, corresponding to the output node.

          model = Sequential()
model.add(Dense(units=1, input_shape=(2,), activation='sigmoid'))

The Dumbo part in Keras constructs a fully connected neural network layer, automatically initializing the weights as biases. Information technology's a super useful part that yous will encounter being used everywhere. The function arguments are divers every bit follows:

units: The first argument, representing number of nodes in this layer. Since nosotros're constructing the output layer, and we said information technology has only one node, this value is 1.
input_shape: The start layer in Keras models need to specify the input dimensions. The subsequent layers (which we don't have here but we volition in later sections) don't need to specify this argument considering Keras can infer the dimensions automatically. In this instance our input dimensionality is ii, the x and y coordinates. The input_shape parameter expects a vector, then in our case information technology'due south a tuple with one number.
activation: The activation function of a logistic regression model is the logistic part, or alternatively called the sigmoid. We will explore dissimilar activation functions, where to use them and why in some other tutorial.

          model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

We so compile the model with the compile function. This creates the neural network model by specifying the details of the learning procedure. The model hasn't been trained yet. Right now we're simply declaring the optimizer to use and the loss function to minimize. The arguments for the compile function are divers equally follows:

optimizer: Which optimizer to apply in order to minimize the loss role. There are a lot of dissimilar optimizers, near of them based on gradient descent. We will explore different optimizers in another tutorial. For now we will apply the adam optimizer, which is the 1 people adopt to utilise by default.
loss: The loss function to minimize. Since we're building a binary 0/1 classifier, the loss function to minimize is binary_crossentropy. We will come across other examples of loss functions in afterward sections.
metrics: Which metric to report statistics on, for classification problems we ready this as accuracy.

          history = model.fit(ten=X, y=y, verbose=0, epochs=50)

Now comes the fun role of actually preparation the model using the fit function. The arguments are as follows:

ten: The input data, we defined it as X above. It contains the x and y coordinates of the input points
y: Not to be confused with the y coordinate of the input points. In all ML tutorials y refers to the labels, in our case the grade nosotros're trying to predict: 0 or one.
verbose: Prints out the loss and accuracy, ready it to 1 to see the output.
epochs: Number of times to go over the entire preparation data. When preparation models we pass through the preparation information not but in one case but multiple times.

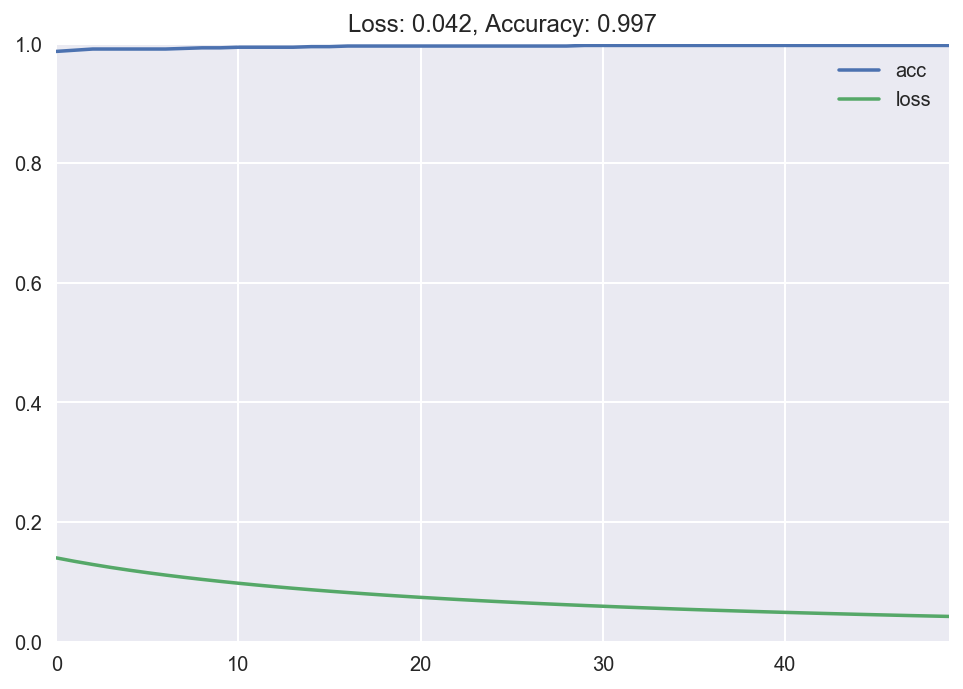
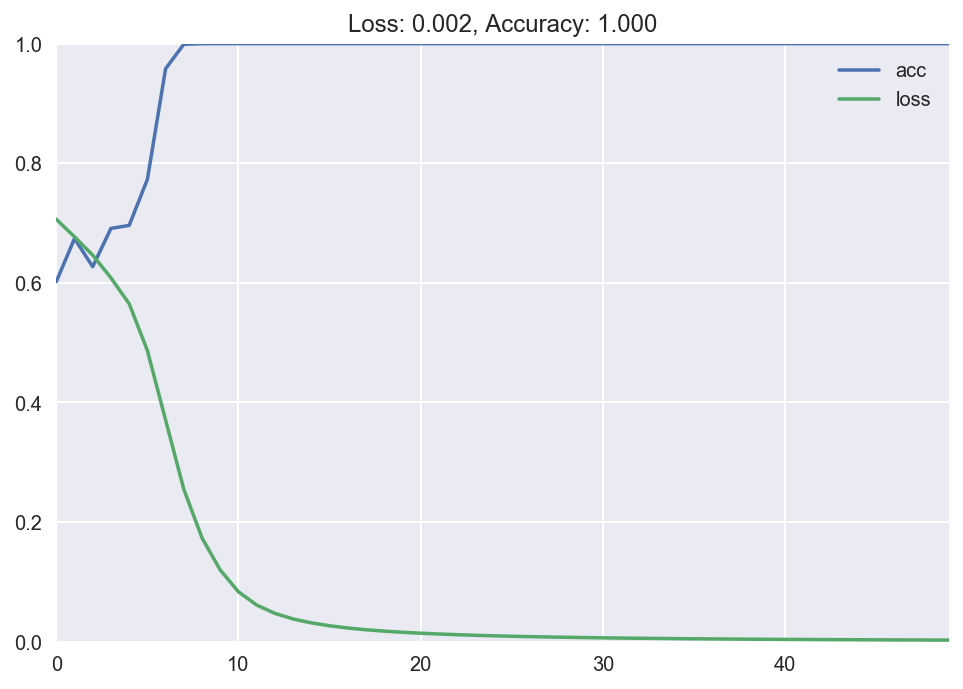
          plot_loss_accuracy(history)

The output of the fit method is the loss and accurateness at every epoch. We so plot it using our custom function, and encounter that the loss goes down to almost 0 over time, and the accuracy goes upwards to nearly 1. Groovy! We have successfully trained our first neural network model with Keras. I know this was a long explanation, but I wanted to explain what we're doing in detail the first time. Once you lot sympathize what's going on and do a couple of times, all this becomes second nature.

Below is a plot of the decision purlieus. The diverse shades of blue and red represent the probability of a hypothetical point in that area belonging to class 1 or 0. The meridian left area is classified equally grade 1, with the color blueish. The bottom right surface area is classified as form 0, colored as red. And at that place is a transition around the decision boundary. This is a cool way to visualize the decision boundary the model is learning.

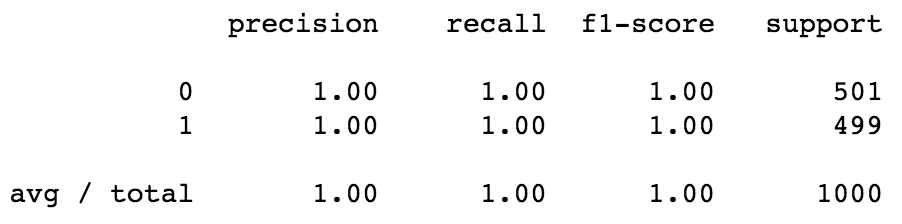
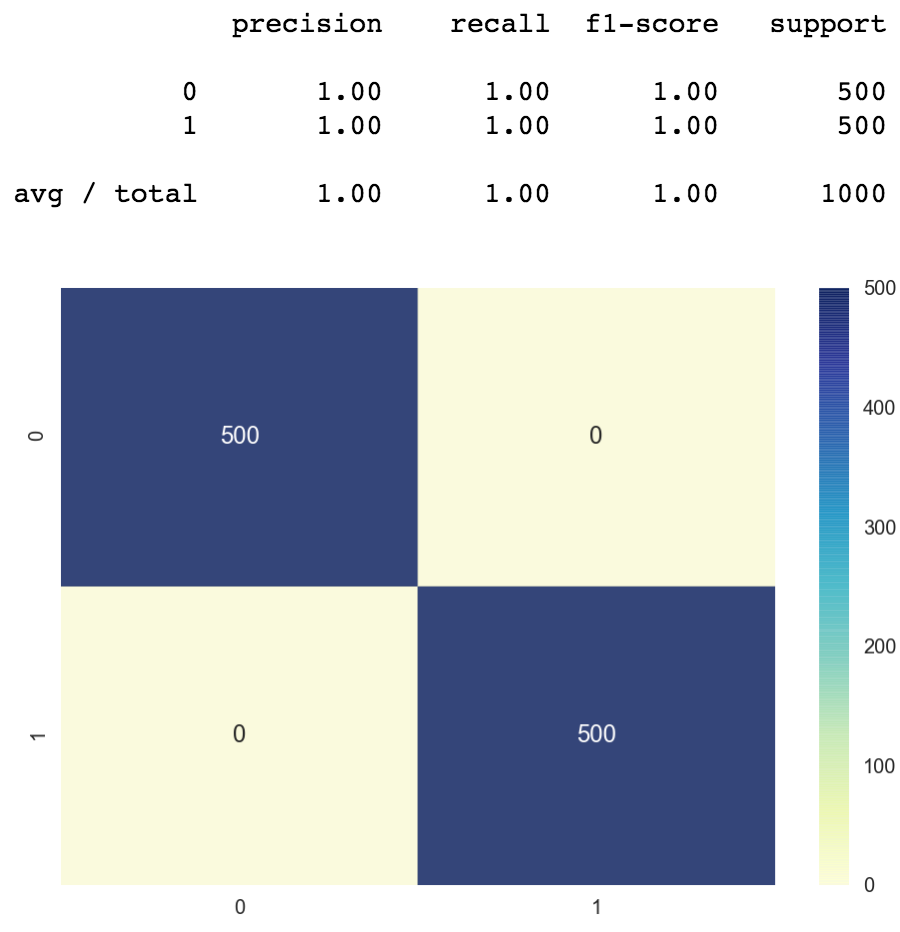
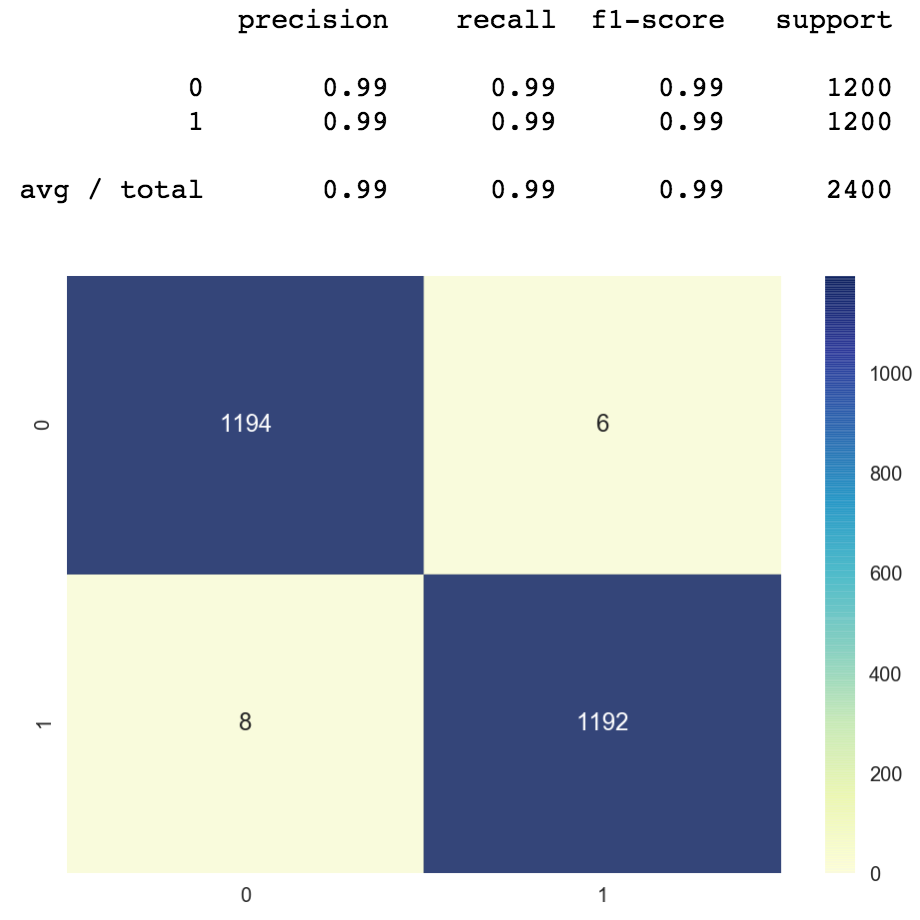
The classification written report shows the precision and recall of our model. We get close to 100% accuracy. The value shown in the report should be 0.997 but it got rounded up to 1.0.

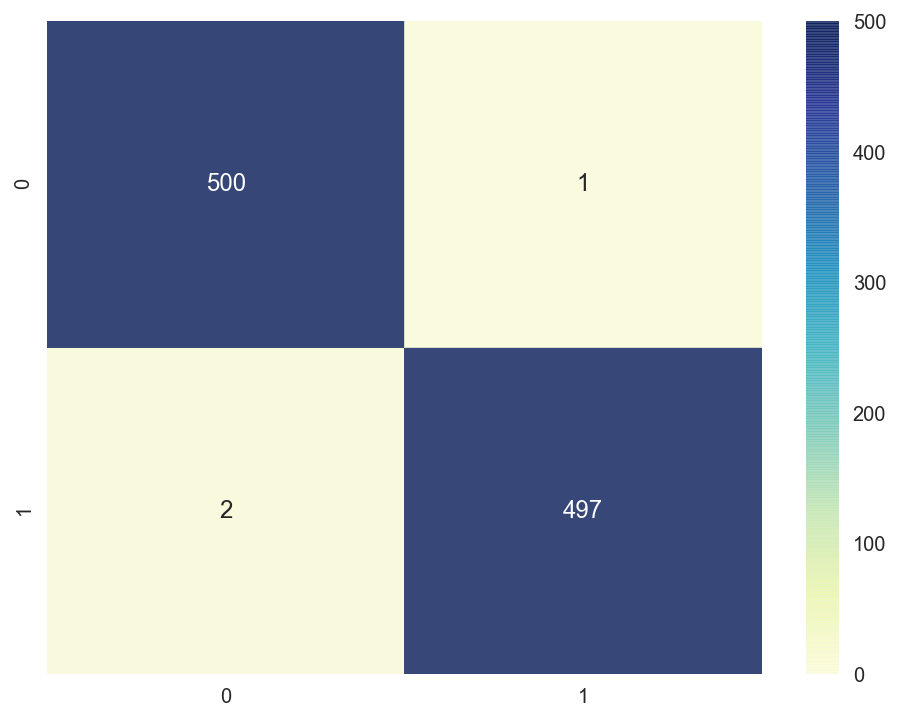
The confusion matrix shows u.s.a. how many classes were correctly classified vs misclassified. The numbers on the diagonal axis represent the number of correctly classified points, the rest are the misclassified ones. This item matrix is not very interesting because the model just misclassifies 3 points. We can see one of the misclassified points at the acme right function of the confusion matrix, the truthful value is class 0 simply the predicted value is class i.

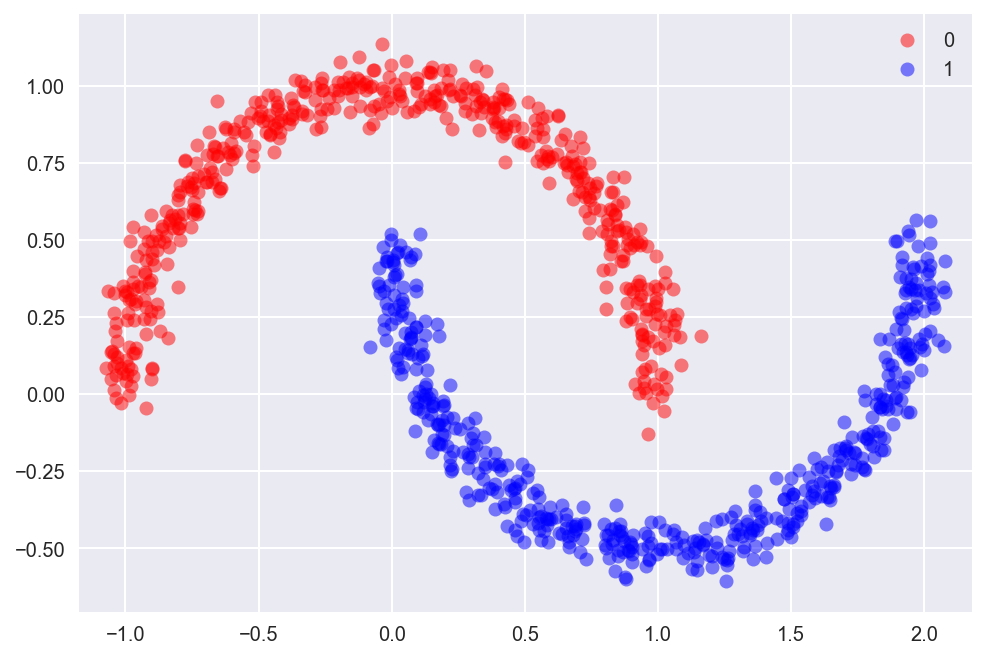
ii.2) Circuitous Data - Moons

The previous dataset was linearly separable, so it was petty for our logistic regression model to separate the classes. Here is a more complex dataset which isn't linearly separable. The unproblematic logistic regression model won't exist able to clearly distinguish between the classes. We're using the make_moons method of scikit-acquire to generate the data.

Let's build another logistic regression model with the same parameters every bit we did before. On this dataset nosotros become 86% accuracy.

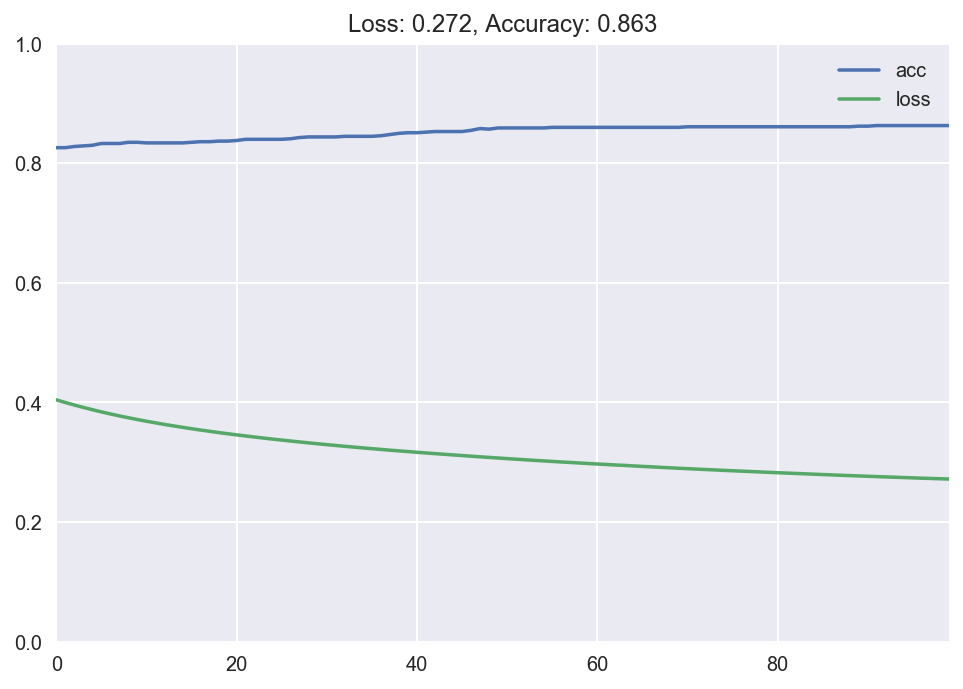
The current conclusion boundary doesn't look every bit clean as the one earlier. The model tried to split out the classes from the centre, but in that location are a lot of misclassified points. We need a more complex classifier with a not-linear decision boundary, and we will run across an example of that presently.

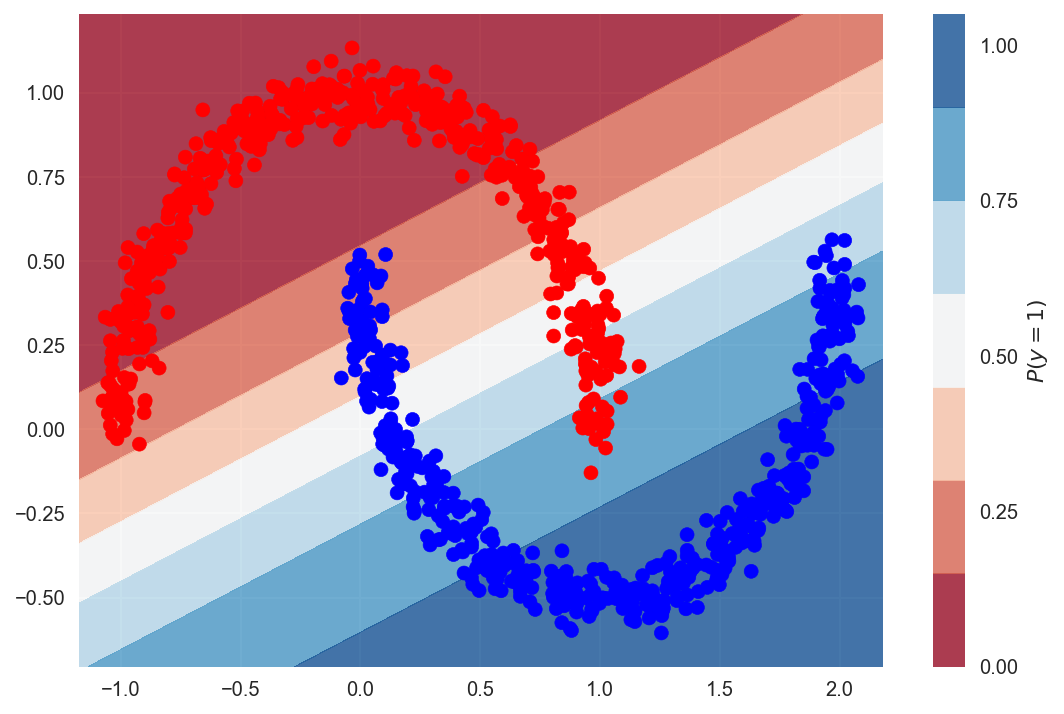
Precision of the model is 86%. It looks good on paper but we should easily be able to get 100% with a more complex model. You tin can imagine a curved decision boundary that will separate out the classes, and a complex model should be able to gauge that.

The classification written report and the confusion matrix looks as follows.

2.3 Circuitous Data - Circles

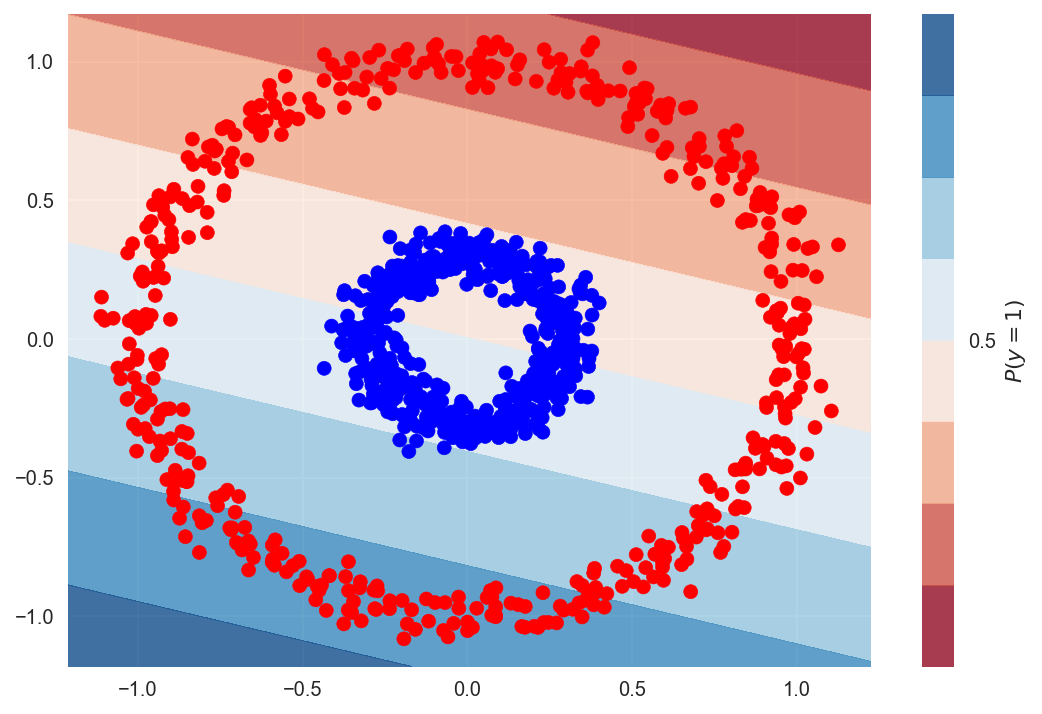
Let's await at i last example where the liner model will fail. This time using the make_circles function in scikit-larn.

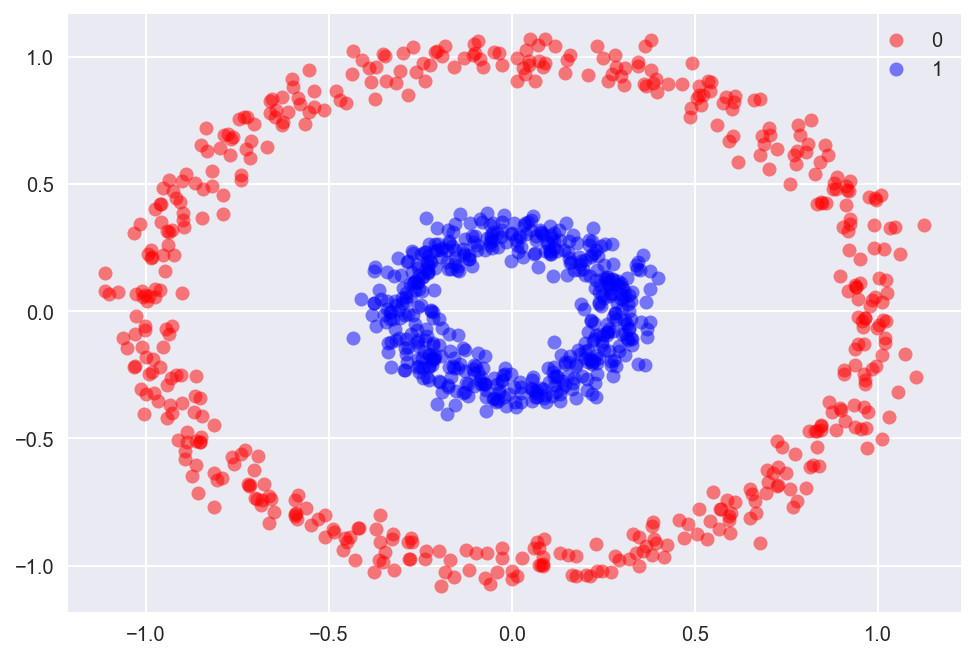
Edifice the model with same parameters.

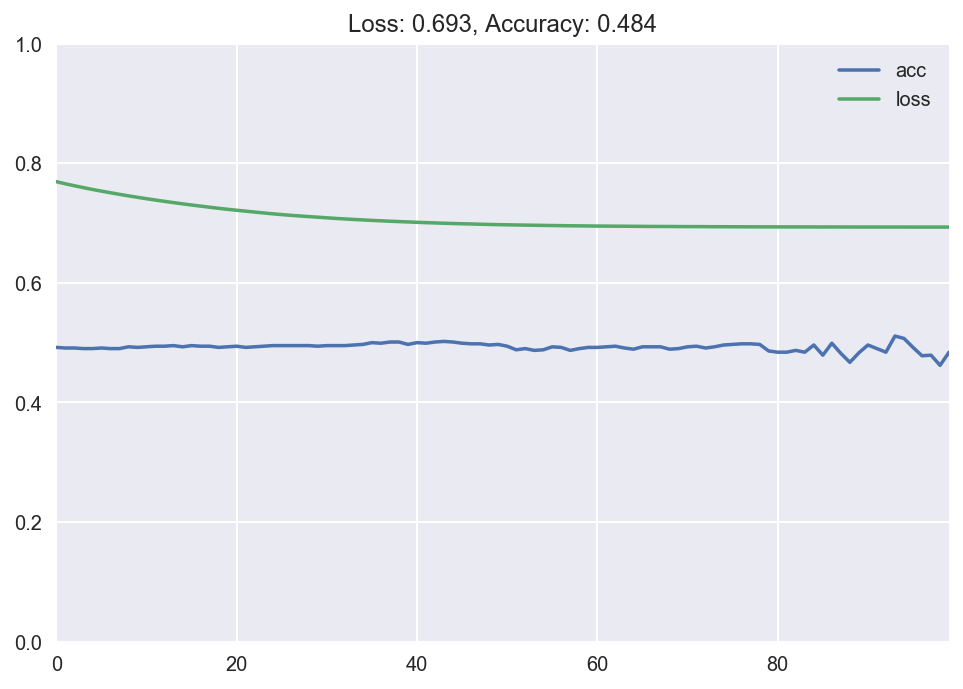
The decision boundary once more passes from the middle of the data, but now we have much more misclassified points.

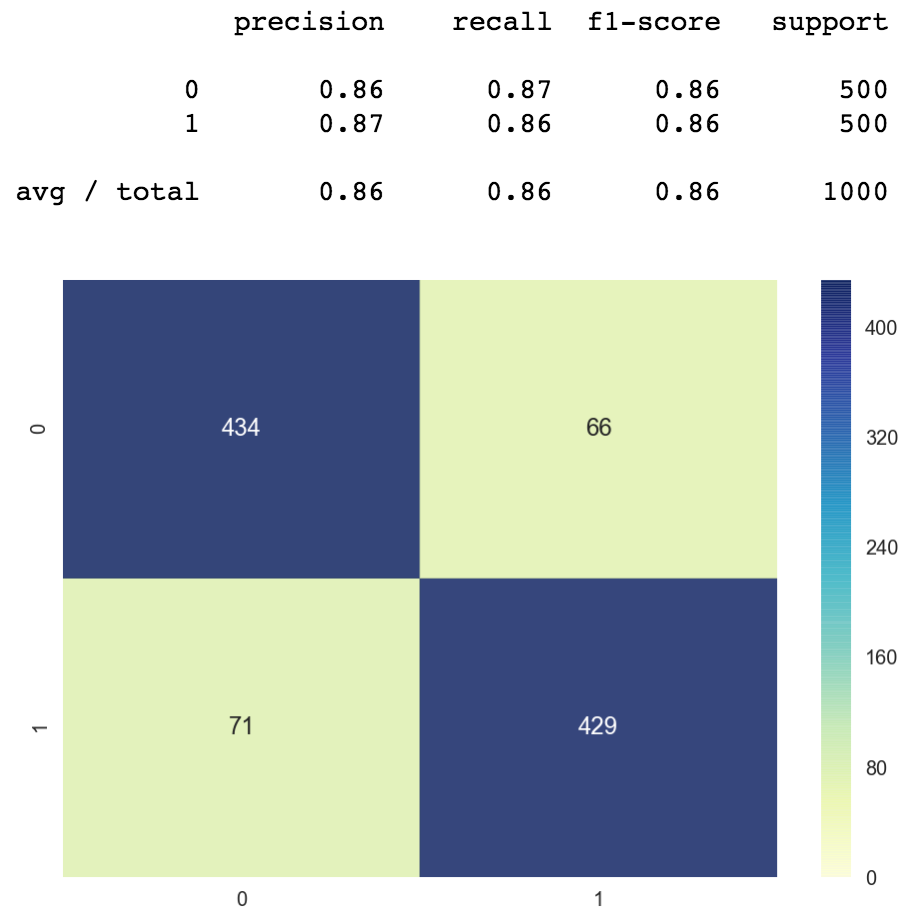
The accurateness is effectually fifty%, shown below. No matter where the model draws the line, it will misclassify half of the points, due to the nature of the dataset.

The defoliation matrix we see here is an example one belonging to a poor classifier. Ideally we prefer confusion matrices to look like the ones we saw to a higher place. Loftier numbers along the diagonals meaning that the classifier was right, and depression numbers everywhere else where the classifier was wrong. In our visualization, the colour blue represents large numbers and yellow represents the smaller ones. So we would prefer to see bluish on the diagonals and yellowish everywhere else. Blueish colour everywhere is a bad sign meaning that our classifier is confused.

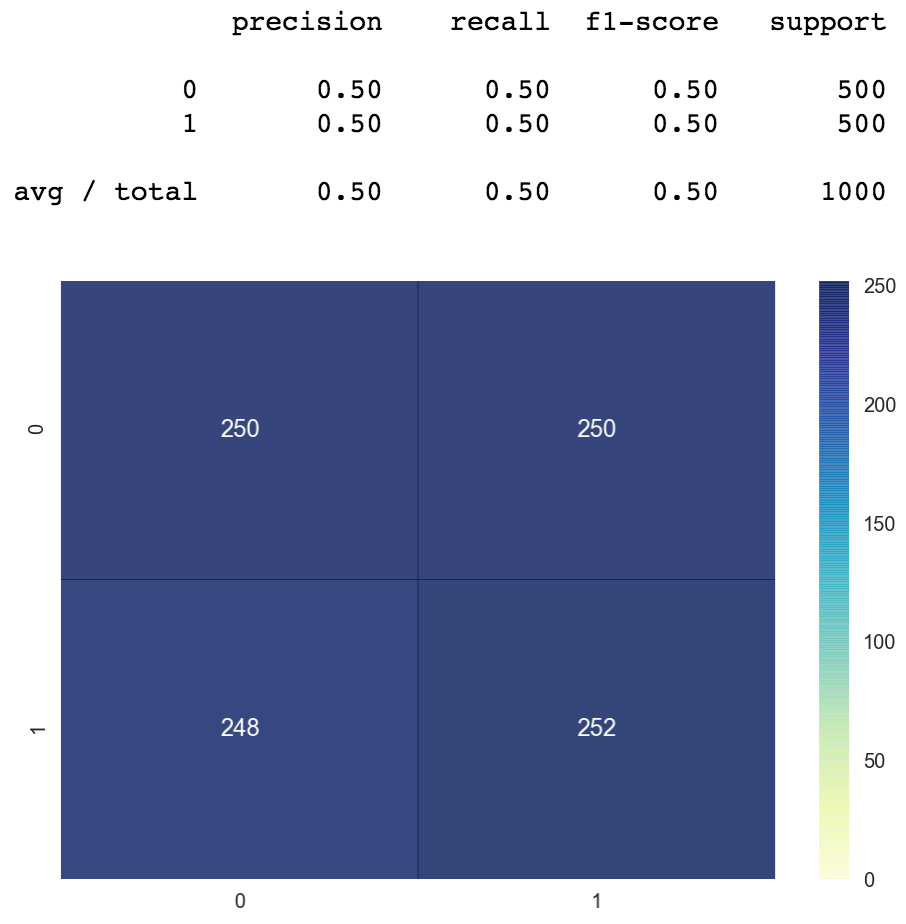
The well-nigh naive method which always predicts one no thing what the input is would go a 50% accuracy. Our model besides got 50% accuracy, so information technology's not useful at all.

three. Artificial Neural Networks (ANN)

At present nosotros volition train a deep Artificial Neural Networks (ANN) to better classify the datasets which the logistic regression model struggled, Moons and Circles. Nosotros will besides classify an fifty-fifty harder dataset of Sine Wave to demonstrate that ANN can class really complex decision boundaries.

3.1) Complex Information - Moons

While building Keras models for logistic regression above, nosotros performed the following steps:

Pace 1: Define a Sequential model.
Pace two: Add a Dense layer with sigmoid activation function. This was the just layer we needed.
Step 3: Compile the model with an optimizer and loss function.
Step 4: Fit the model to the dataset.
Step 5: Analyze the results: plotting loss/accuracy curves, plotting the conclusion boundary, looking at the nomenclature report, and agreement the defoliation matrix.

While building a deep neural network, nosotros only need to change pace 2 such that, nosotros will add several Dumbo layers i after another. The output of ane layer becomes the input of the next. Keras once again does most of the heavy lifting by initializing the weights and biases, and connecting the output of i layer to the input of the side by side. We just need to specify how many nodes nosotros want in a given layer, and the activation part. Information technology'south as simple equally that.

We starting time add a layer with 4 nodes and tanh activation function. Tanh is a usually used activation function, and nosotros'll learn more than virtually information technology in some other tutorial. We and then add another layer with 2 nodes again using tanh activation. Nosotros finally add the last layer with one node and sigmoid activation. This is the final layer that we as well used in the logistic regression model.

This is non a very deep ANN, it only has three layers: 2 hidden layers, and the output layer. Only discover a couple of patterns:

Output layer still uses the sigmoid activation function since we're working on a binary classification trouble.
Subconscious layers use the tanh activation function. If we added more subconscious layers, they would also apply tanh activation. Nosotros take a couple of options for activation functions: sigmoid, tanh, relu, and variants of relu. In some other article we'll explore the pros and cons of each one. We volition besides demonstrate why using sigmoid activation in subconscious layers is a bad thought. For at present it'south safety to employ tanh.
We have fewer number of nodes in each subsequent layer. It's mutual to have less nodes equally nosotros stack layers on top of one some other, sort of a triangular shape.

We didn't build a very deep ANN hither considering it wasn't necessary. Nosotros already achieve 100% accuracy with this configuration.

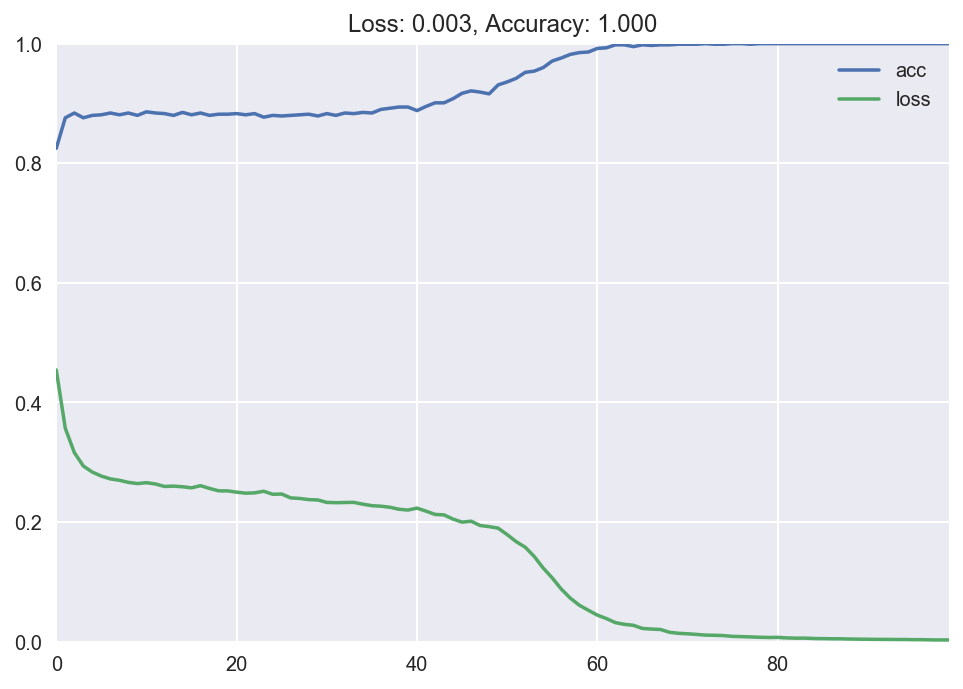
The ANN is able to come with a perfect separator to distinguish the classes.

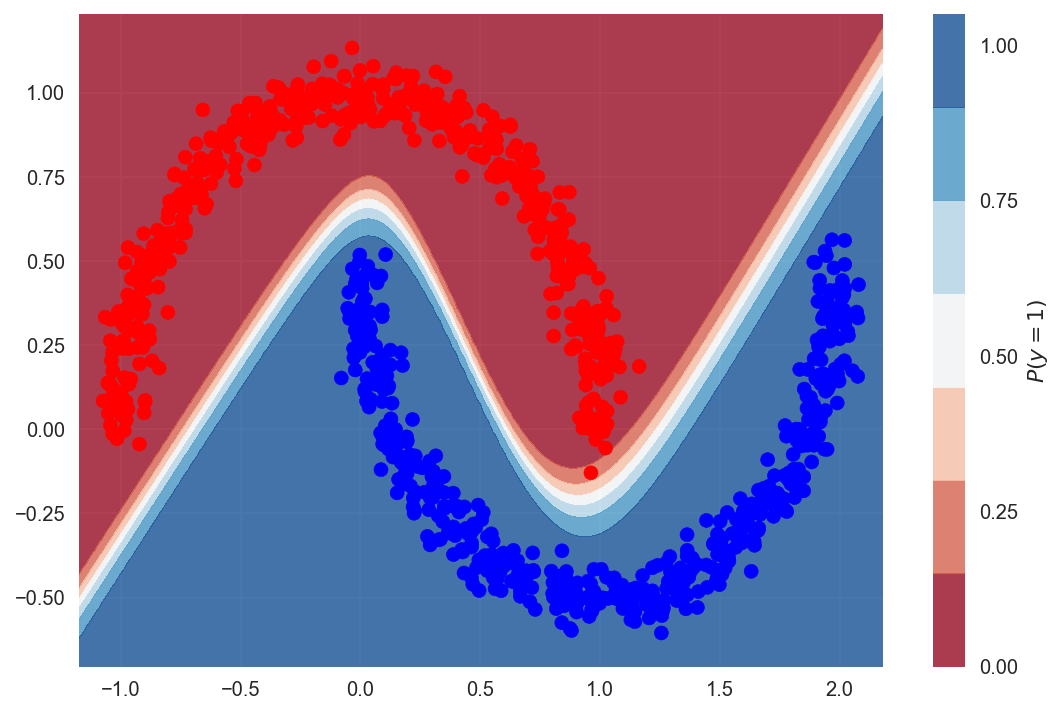
100% precision, cypher misclassified.

3.two) Complex Data - Circles

Now allow'southward look at the Circles dataset, where the LR model achieved only 50% accuracy. The model is the same as in a higher place, we only modify the input to the fit function using the electric current dataset. And we once more accomplish 100% accurateness.

Similarly the determination boundary looks simply similar the one we would draw by hand ourselves. The ANN was able to effigy out an optimal separator.

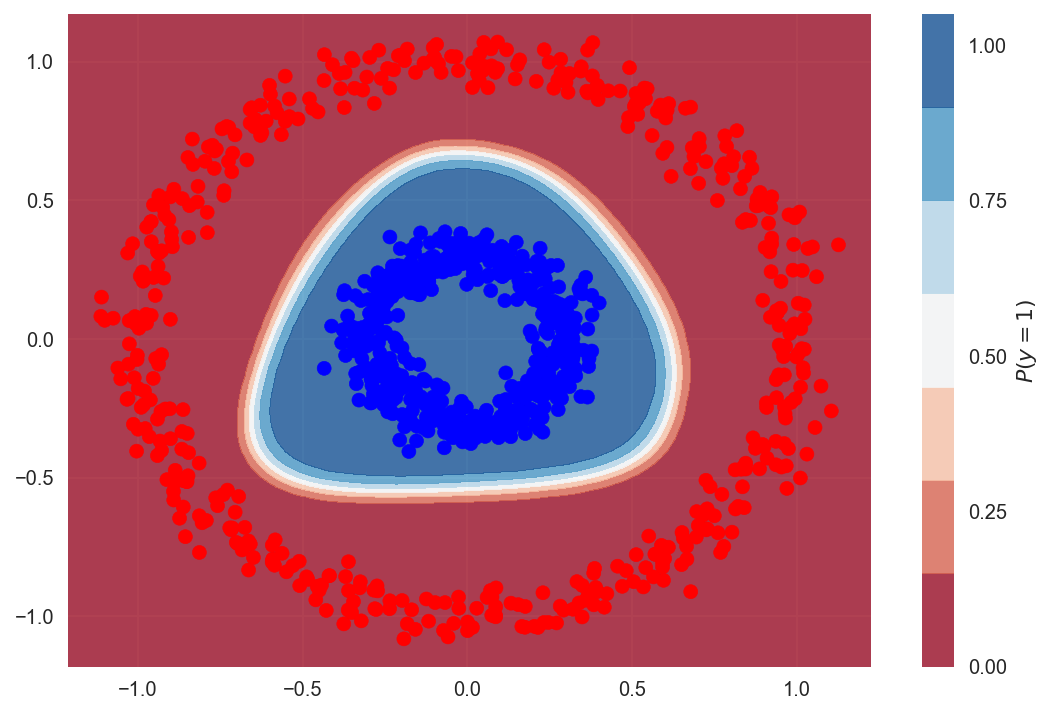
Simply like higher up we go 100% accurateness.

4.three) Complex Data - Sine Wave

Permit'due south try to classify i final toy dataset. In the previous sections, the classes were separable by 1 continuous determination purlieus. The boundary had a complex shape, it wasn't linear, only still 1 continuous determination boundary was plenty. ANN can draw capricious number of complex decision boundaries, and we will demonstrate that.

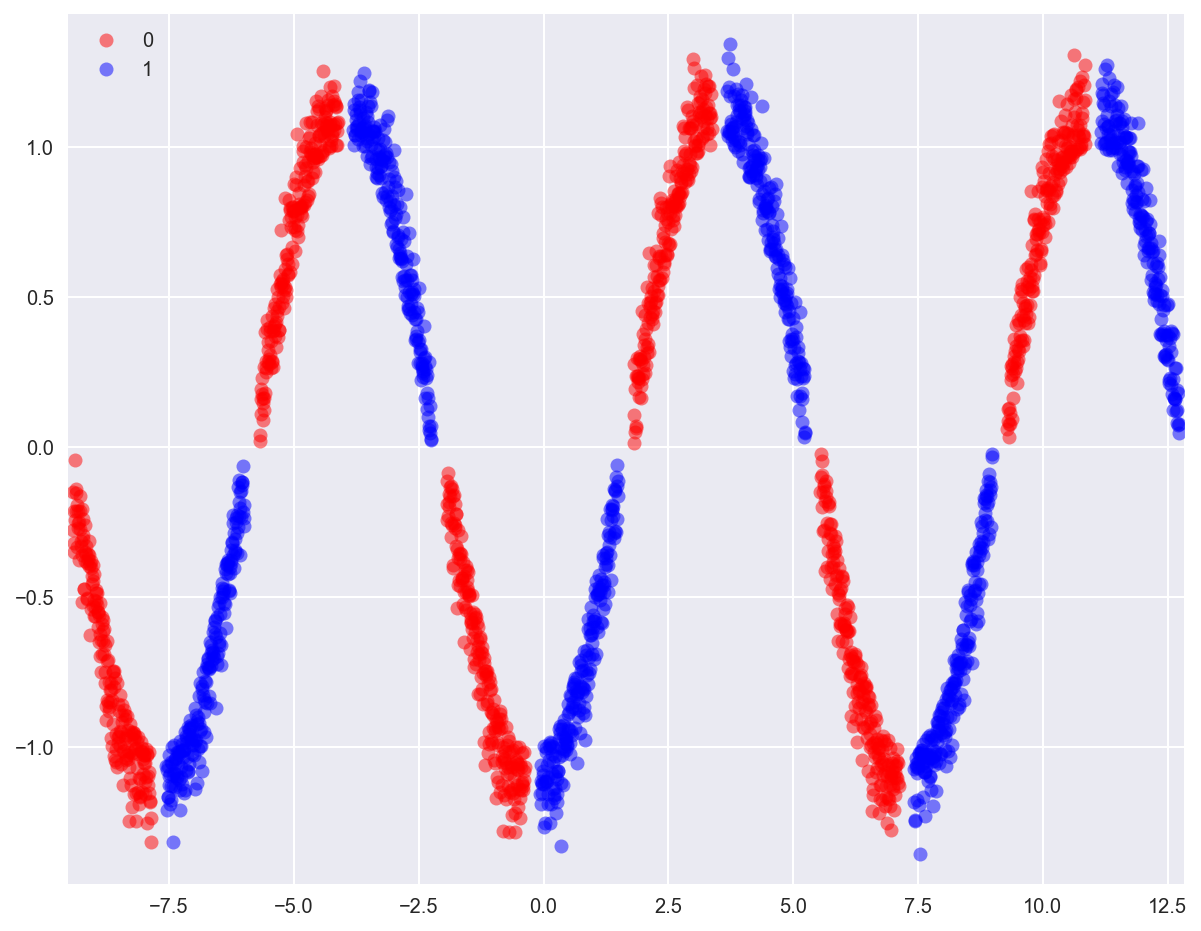
Let'southward create a sinusoidal dataset looking like the sine part, every up and downwardly belonging to an alternate class. As we can run across in the figure, a single decision boundary won't be able to separate out the classes. We will need a series of non-linear separators.

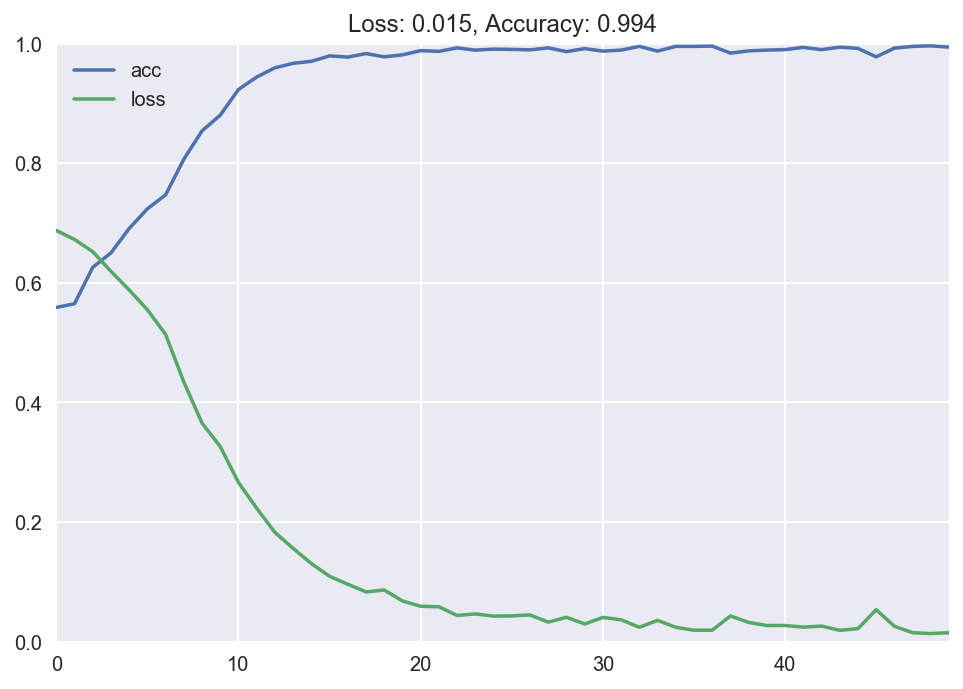
Now nosotros demand a more complex model for accurate classification. And then we have iii subconscious layers, and an output layer. The number of nodes per layer has as well increased to improve the learning capacity of the model. Choosing the right number of hidden layers and nodes per layer is more of an fine art than science, usually decided past trial and error.

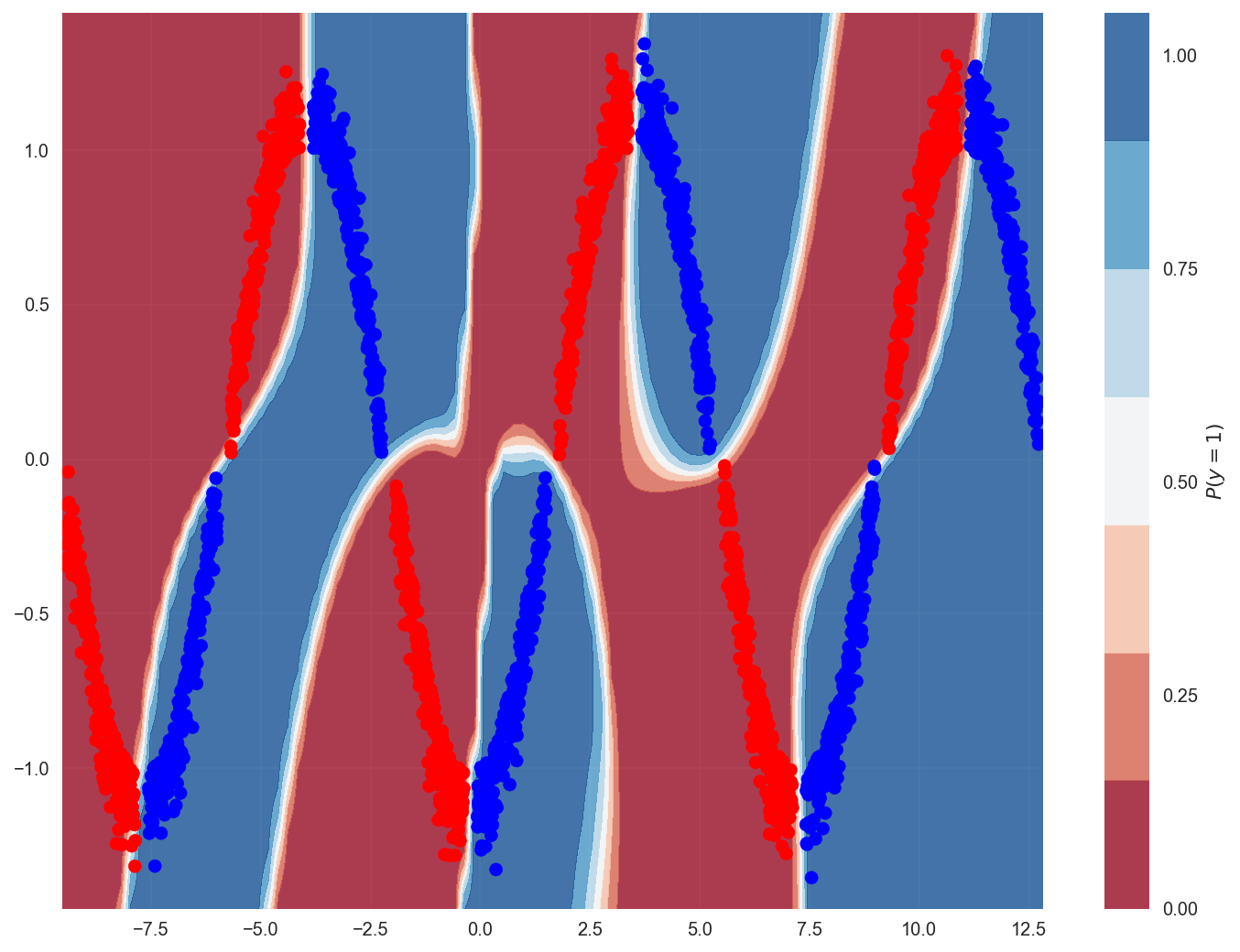
The ANN was able to model a pretty complex gear up of decision boundaries.

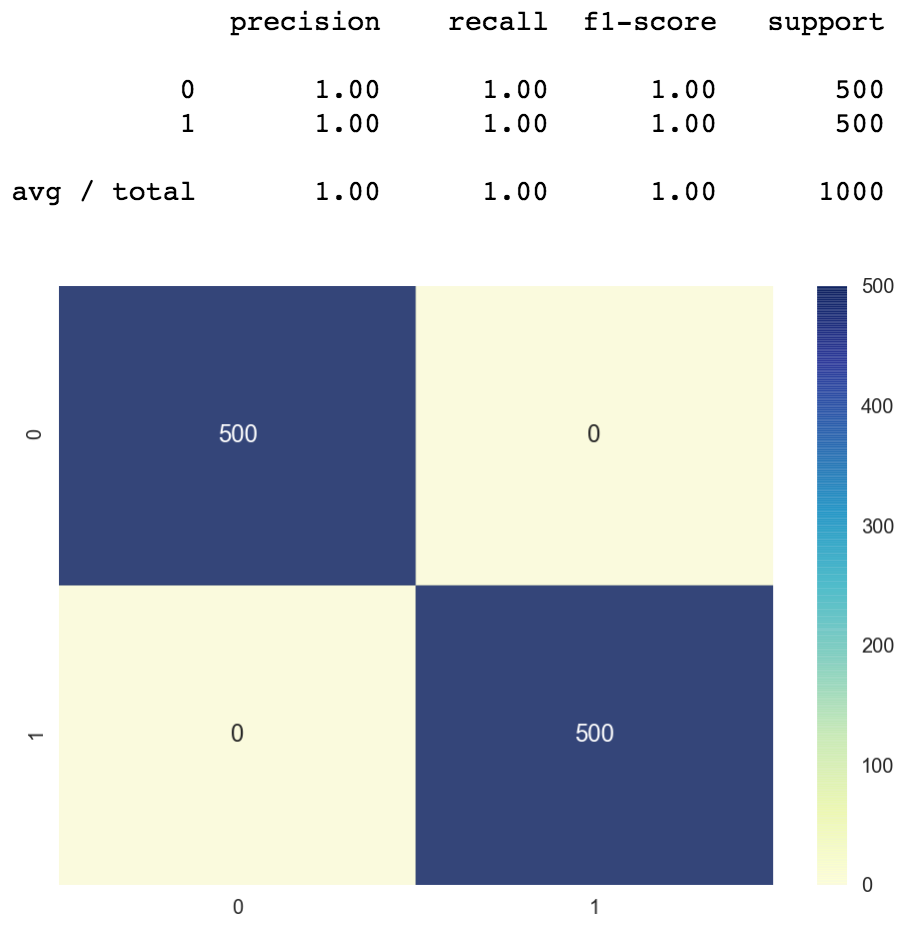
Precision is 99%, we only accept 14 misclassified points out of 2400. Pretty practiced.

4. Multiclass Classification

In the previous sections we worked on binary nomenclature. Now we volition accept a await at a multi-class classification problem, where the number of classes is more 2. We volition selection 3 classes for demonstration, but our approach generalizes to whatsoever number of classes.

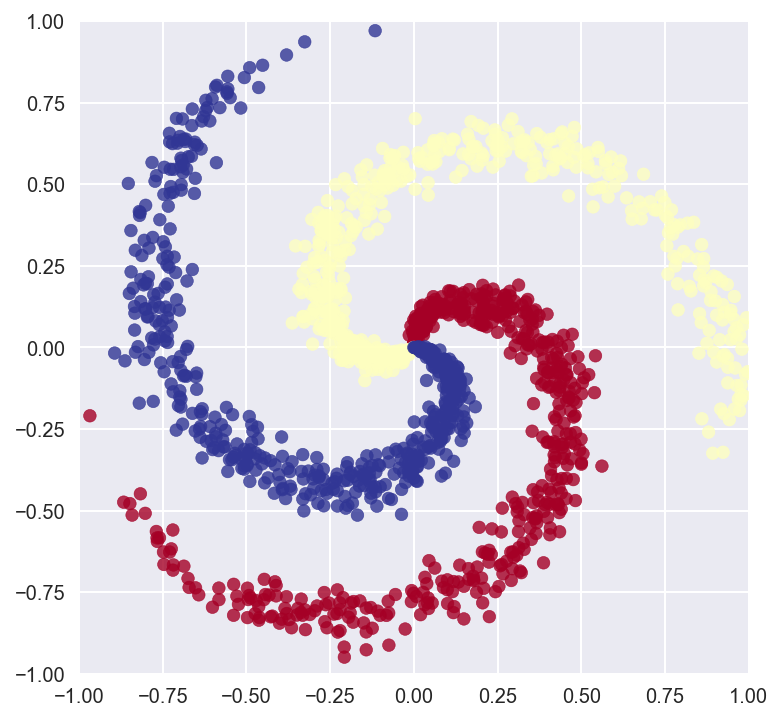
Here'south how our dataset looks like, screw data with 3 classes, using the make_multiclass method in scikit-acquire.

4.1) Softmax Regression

Every bit we saw above, Logistic Regression (LR) is a classification method for ii classes. It works with binary labels 0/i. Softmax Regression (SR) is a generalization of LR where we tin have more than ii classes. In our electric current dataset we have iii classes, represented equally 0/1/two.

Edifice the model for SR is very similar to LR, for reference hither's how we congenital our Logistic Regression model.

And here's how how nosotros will build the Softmax Regression model.

There are a couple of differences, allow'due south go over them one past one:

Number of nodes in the dumbo layer: LR uses 1 node, where SR has three nodes. Since we accept 3 classes it makes sense for SR to be using 3 nodes. Then the question is, why does LR uses but 1 node, information technology has 2 classes so information technology appears like we should have used 2 nodes instead. The respond is, considering we can attain the same result with using just one node. As we saw to a higher place, LR models the probability of an example belonging to grade one: P(class=one). And we tin summate grade 0 probability by: one−P(class=one). But when we have more than two classes, we need individual nodes for each grade. Considering knowing the probability of i form doesn't let us infer the probability of the other classes.
Activation function: LR used sigmoid activation role, SR uses softmax. Softmax scales the values of the output nodes such that they represent probabilities and sum up to one. So in our case P(class=0)+P(class=1)+P(form=2)=ane. Information technology doesn't do it in a naive style past dividing individual probabilities past the sum though, it uses the exponential role. So higher values go emphasized more than and lower values get squashed more. We volition talk in item what softmax does in another tutorial. For now you can simply think of it as a normalization office which lets usa translate the output values as probabilities.
Loss function: In a binary nomenclature trouble like LR, the loss office is binary_crossentropy. In the multiclass case, the loss role is categorical_crossentropy. Categorical crossentropy is the generalization of binary crossentropy to more than 2 classes. Going into the theory behind loss functions is beyond the scope of this tutorial. But for now only knowing this holding is enough.
Fit part: LR used the vector y direct in the fit function, which has just ane column with 0/1 values. When we're doing SR the labels need to be in one-hot representation. In our example y_cat is a matrix with iii columns, where all the values are 0 except for the one that represents our class, and that is 1.

It took some time to talk about all the differences between LR and SR, and it looks like there'south a lot to digest. But again after some practice this will get a habit, and you won't fifty-fifty need to think virtually any of this.

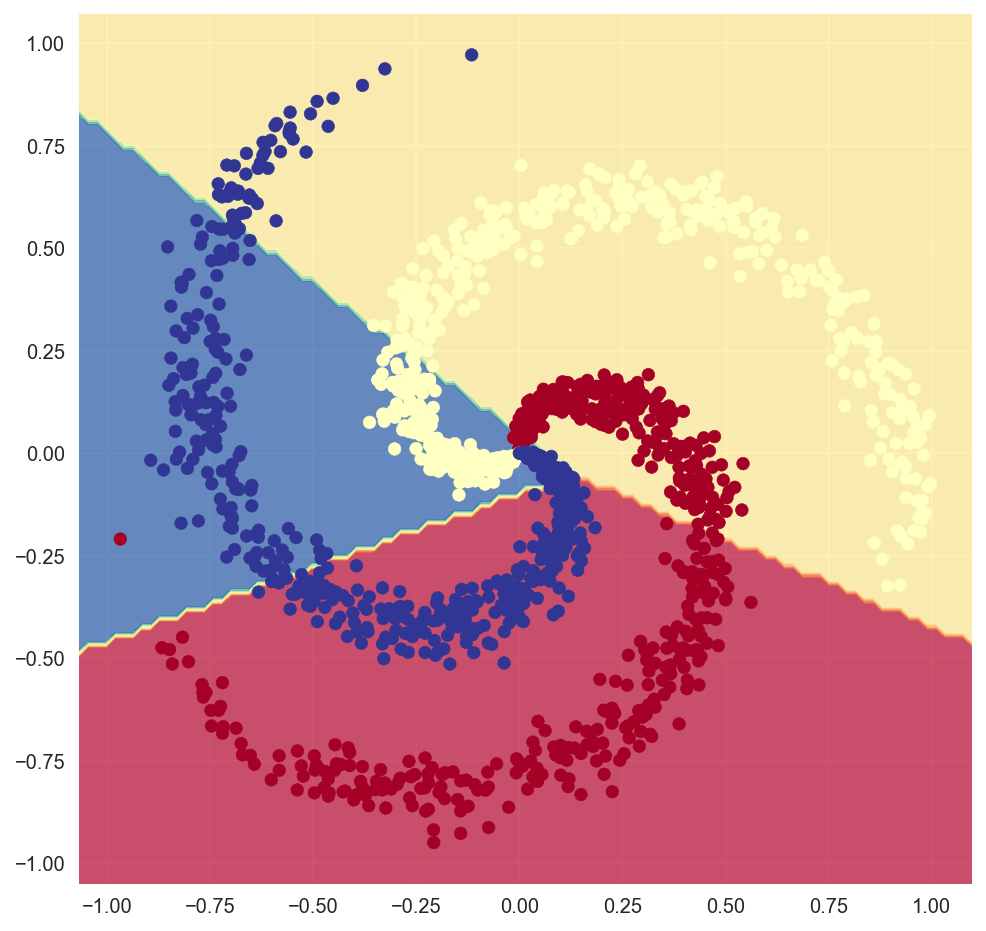
After all this theory let's have a step back and think that LR is a linear classifier. SR is as well a linear classifier, but for multiple classes. So the "power" of the model hasn't inverse, it's still a linear model. Nosotros just generalized LR to utilize it to a multiclass problem.

Training the model gives us an accuracy of around 50%. The nearly naive method which always predicts class 1 no matter what the input is would have an accuracy of 33%. The SR model is non much of an comeback over it. Which is expected because the dataset is non linearly separable.

Looking at the conclusion boundary confirms that nosotros withal have a linear classifier. The lines expect jagged due to floating point rounding but in reality they're direct.

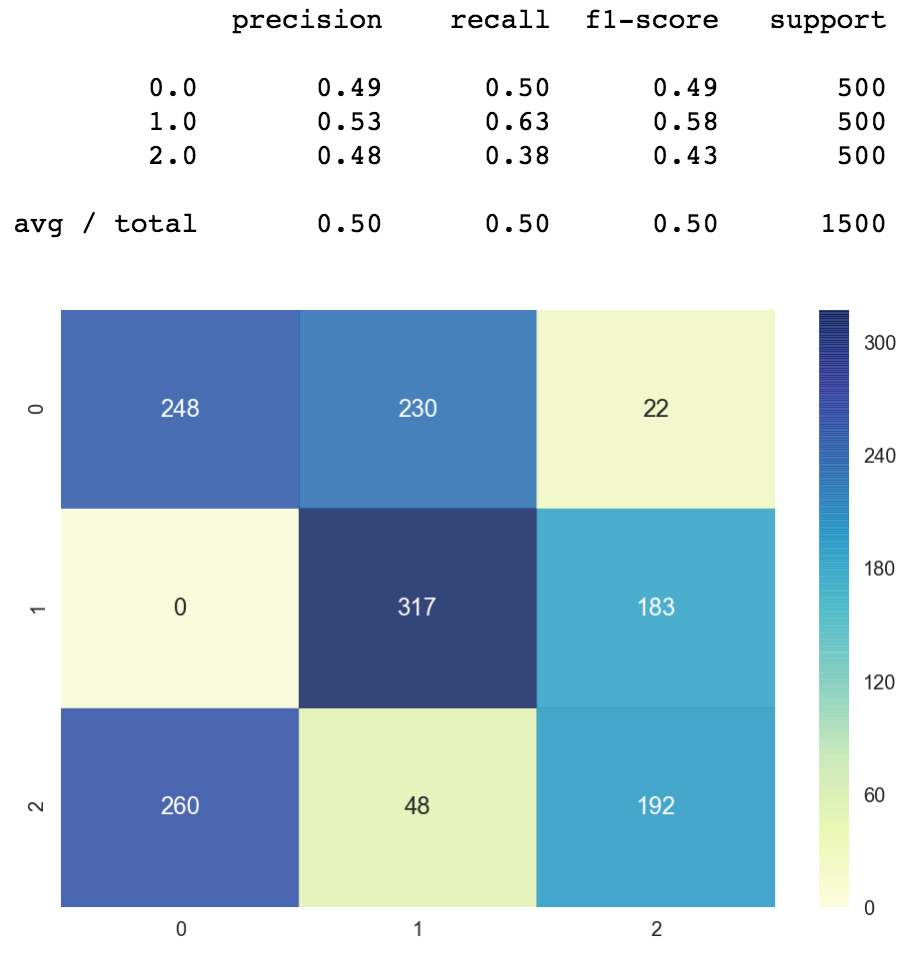
Here'south the precision and call back corresponding to the 3 classes. And the confusion matrix is all over the place. Clearly this is not an optimal classifier.

iv.2) Deep ANN

At present let'south build a deep ANN for multiclass classification. Recollect that the changes going from LR to ANN was minimal. We only needed to add more Dumbo layers. We will practice the same again. Adding a couple of Dumbo layers with tanh activation function.

Note that the output layer still has 3 nodes, and uses the softmax activation. The loss function also didn't change, all the same categorical_crossentropy. These won't change going from a linear model to a deep ANN, since the problem definition hasn't changed. We're still working on multiclass nomenclature. Only at present using a more than powerful model, and that power comes from adding more than layers to our neural net.

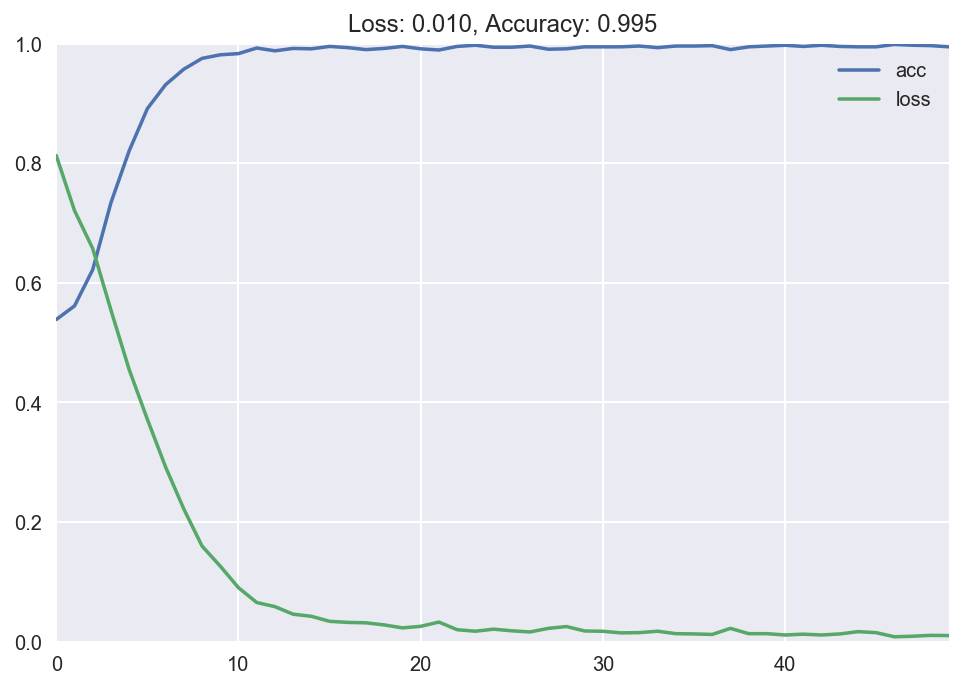
We achieve 99% accuracy in just a couple of epochs.

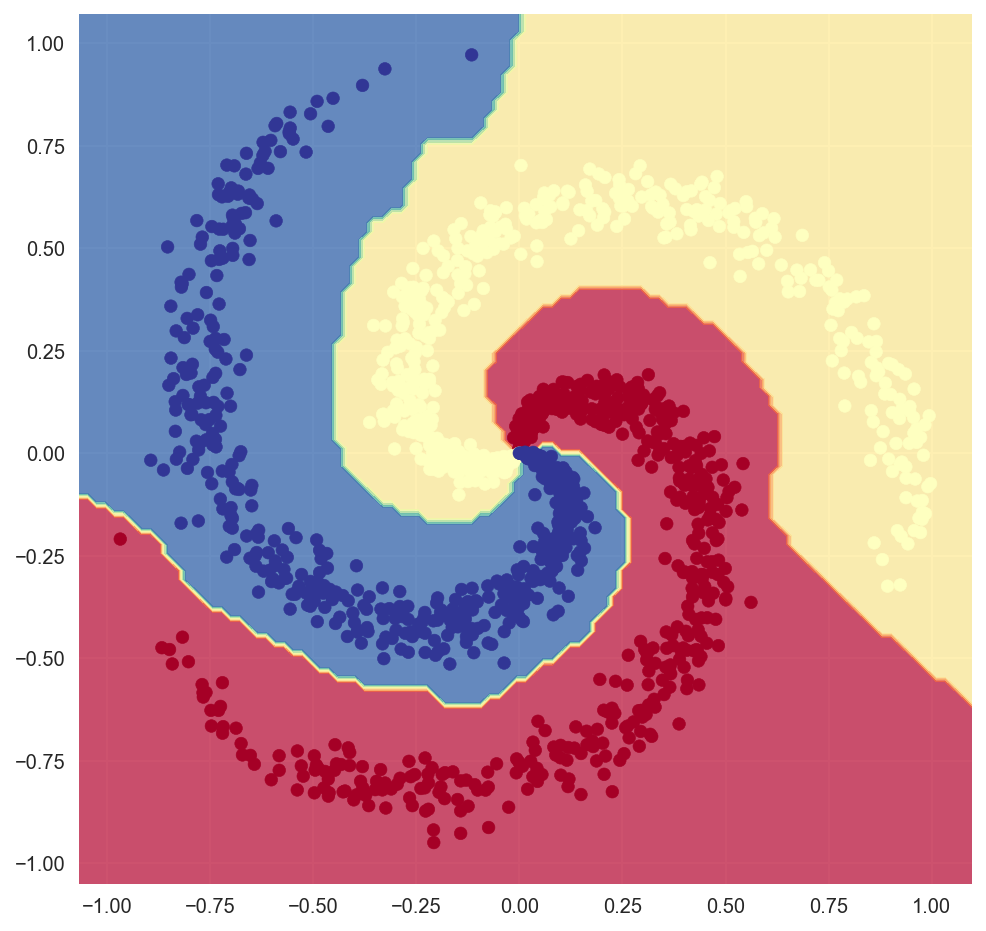
The decision purlieus is non-linear.

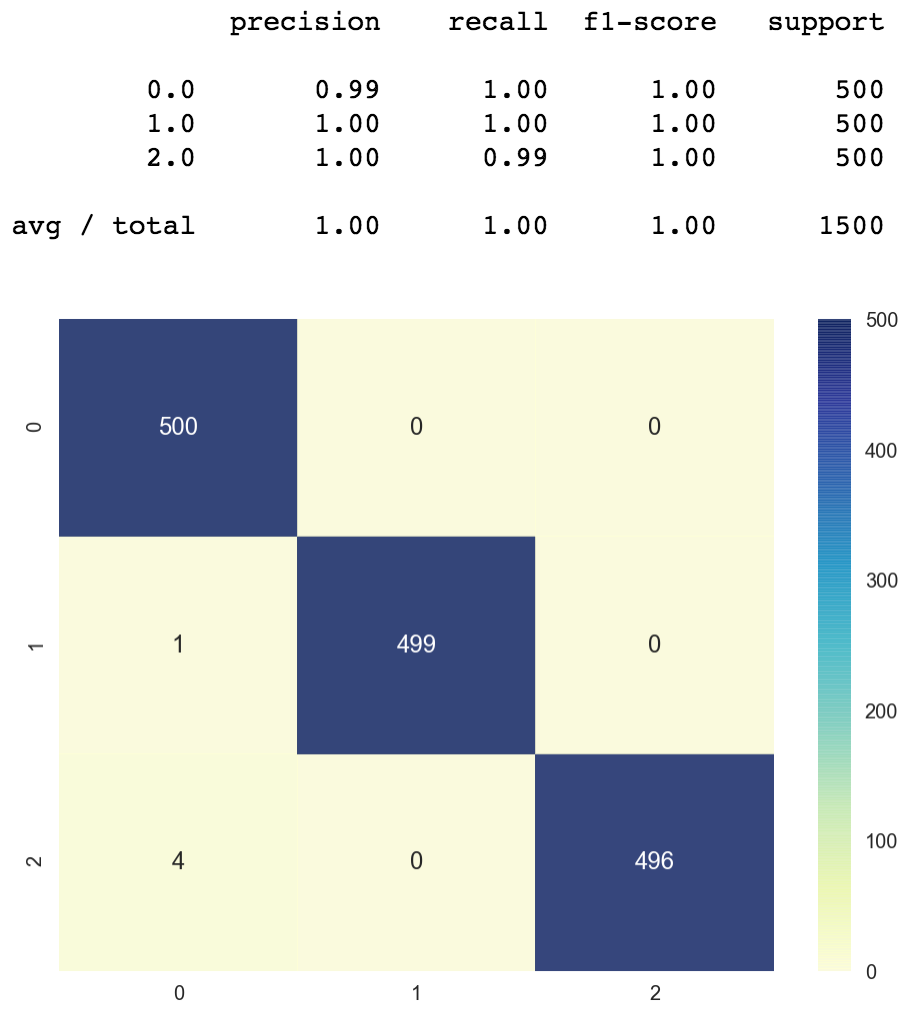
We got about 100% accuracy. We totally misclassified 5 points out of 1500.

5) Determination

Thank you for spending fourth dimension reading this commodity, I know this was a rather lengthy tutorial on Artificial Neural Networks and Keras. I wanted to be every bit detailed equally possible, while nevertheless keeping the article length manageable. I promise you enjoyed it.

In that location was a common theme in this article such that nosotros start introduced the chore, we then approached it using a uncomplicated method and observed the limitations. Afterward we used a more complex deep model to amend on it and got much amend results. I recall the ordering is of import. No complex method becomes successful unless it has evolved from a simpler model.

The entire code for this article is available here if you want to hack on it yourself. If you have any feedback feel free to reach out to me on twitter.

springerausand.blogspot.com

Source: https://towardsdatascience.com/applied-deep-learning-part-1-artificial-neural-networks-d7834f67a4f6